Место для рекламы
Загадка - «В одном буддийском храме на высоте 100 м…»
Админ
10 Апреля 2015
Загадка №3980.
В одном буддийском храме на высоте 100 метров к потолку приделаны два золотых каната, длиной по 100 метров каждый.Оба каната свисают до пола. Они висят на близком расстоянии, например, - полметра. В храм заходит Вор - ловкий акробат, который умеет лазить по канатам и отрезать их. Если Вор свалится на землю с высоты менее 10 метров, то он доволен. Если с большей высоты – умирает (лечение ему уже не поможет).
Как ему удалось забрать из храма не менее 190 метров золотого каната, а не только 110? (канаты считать легкими).
Ответ: Влезает по одному из канатов на высоту 95 метров и отрезает от другого 95 метров. Часть в 5 метров, которая осталась висеть, привязывает к первому канату в точке деления на 5 и 95 метров. Выходит, петля создана связанными 5 метрами первого каната и 5 метрами второго каната. После чего, свободный конец полученного 195 метрового каната пропускает через петлю. Вверху он режет первый канат в точке 5 и 95 метров. Выходит, что через петлю 10 метров свисает канат длиной 190 метров. Вор спускается вниз и забирает 190 метров.
Комментарии
Похожие загадки
Валентин
28 Апреля 2015
Загадка №4036.
Во время летнего пикника четыре супружеские пары выпили 32 бутылки лимонада. Жены выпили: Жанна – 1 бутылку, Жаклин – 2 бутылки, Колетта – 3 бутылки и Анетта – 4 бутылки. Мужья не уступили женам: месье Пон выпил столько же, сколько его жена, месье Дюбуа – вдвое больше своей жены, месье Пейзан – втрое и месье Фонтен – вчетверо больше своих жен.Как зовут мадам Пон, Дюбуа, Пейзан и Фонтен?
Ответ: Пусть х, у, z и u – число бутылок лимонада, которое выпили соответственно жены месье Попа, Дюбуа, Пейзана и Фонтена. Всего жены выпили
х + у + z + u = 10
бутылок лимонада. Их мужья выпили
х + 2у + 3z + 4u
бутылок лимонада, а четыре супружеские пары вместе опустошили
2х +3 у + 4z + 5u = 32
бутылки лимонада. Подставляя
u = 10 - х - у - z, получаем
18 = 3х+2 у + z .
Числа х и z должны быть либо оба четными, либо оба нечетными. Значения х=1 и х=2 отпадают, так как каждое из чисел у и z не превосходит 4. При х=4 мы получили бы z = 2 и у = 2, что невозможно, так как х, у, z и u – различные числа. Следовательно, задача допускает единственное решение:
х = 3, z = 1, у = 4, u = 2;
х = 3 (Колетта Пон), у = 4 (Анетта Дюбуа), z = 1 (Жанна Пейзан), u = 2 (Жаклин Фонтен).
х + у + z + u = 10
бутылок лимонада. Их мужья выпили
х + 2у + 3z + 4u
бутылок лимонада, а четыре супружеские пары вместе опустошили
2х +3 у + 4z + 5u = 32
бутылки лимонада. Подставляя
u = 10 - х - у - z, получаем
18 = 3х+2 у + z .
Числа х и z должны быть либо оба четными, либо оба нечетными. Значения х=1 и х=2 отпадают, так как каждое из чисел у и z не превосходит 4. При х=4 мы получили бы z = 2 и у = 2, что невозможно, так как х, у, z и u – различные числа. Следовательно, задача допускает единственное решение:
х = 3, z = 1, у = 4, u = 2;
х = 3 (Колетта Пон), у = 4 (Анетта Дюбуа), z = 1 (Жанна Пейзан), u = 2 (Жаклин Фонтен).
Любитель загадок
14 Февраля 2018
Загадка №6815.
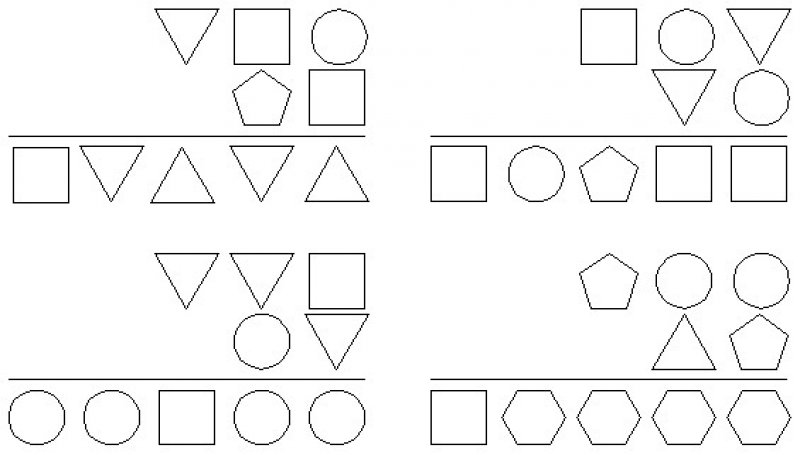
Ответ: Квадрат - 2, круг - 8, треугольник - 6, перевернутый треугольник - 9, пятиугольник - 3, шестиугольник - 4.
Любитель загадок
10 Марта 2016
Загадка №4105.
На столе лежит десять пронумерованных шляп. В каждой шляпе лежит по десять золотых монет. В одной из шляп фальшивые монеты. Настоящая монета весит 10 граммов, а поддельная только 9. В помощь даны весы со шкалой в граммах. Как определить в которой из шляп находятся фальшивые монеты, используя весы только для одного взвешивания? Весы могут взвешивать не больше 750 грамм.
Ответ: Из первой шляпы берем одну монету, из второго две, из третьего три и так далее, кладем все эти монеты на весы. Если бы все монеты были настоящими, то вес был бы: 10*(1+2+3+4+5+6+7+8+9+10). Вместе: 550 грамм. Но несколько монет являются фальшивыми, а сколько - легко узнать. Достаточно из 550 отнять тот вес, что мы получили, и мы увидим «погрешность», равную количеству фальшивых монет. Количество монет укажет на шляпу.
Хулиганка
4 Февраля 2015
Загадка №3977.
Три года назад Настя была в 7 раз старше своей сестры Вероники. Два года назад Настя была в 4 раза старше Вероника. Год назад Настя была в 3 раза старше Вероника.Сколько лет Насте и Веронике?
Ответ: Насте 10 лет, а Веронике 4 года. Доказательство: пусть в настоящий момент Насте x лет, а Веронике y. Тогда, три года назад можно было бы записать: x-3=7*(y-3), два года тому назад: x-2=4*(y-2), год назад: x-1=3*(y-1). Из последнего уравнения выплывает, что x=3*y-2. Подставляя это во второе уравнение, получаем: 3*y-2-2=4*(y-2) откуда y=4. Подставляя значение y в уравнение для x, получаем: x=3*4-2=10.
Загадочник
21 Октября 2015
Загадка №4003.
Дерево отбрасывает тень длиной 10 м. Столб длиной 3 м отбрасывает тень длиной 2 м. Чему равняется высота дерева?
Ответ: Высота дерева относится к длине тени, что оно отбрасывает, так же, как высота столба к длине своей тени, значит
х : 10 = 3 : 2
х =15.
Отсюда, высота дерева равняется 15 м.
х : 10 = 3 : 2
х =15.
Отсюда, высота дерева равняется 15 м.