Место для рекламы
Яков Исидорович Перельман - «Дачники и коровы»
Любитель загадок
27 Ноября 2024
Дачники и коровы

Ответ: Два варианта решения задачи представлены на рисунке. 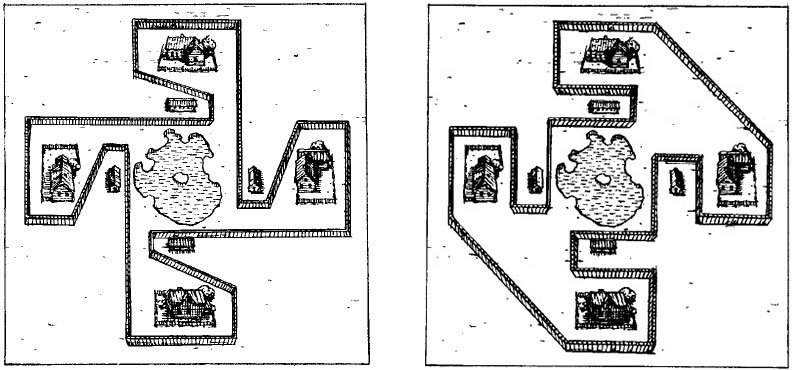

Комментарии
Похожие загадки
Любитель загадок
19 Ноября 2024
Белки и кролики
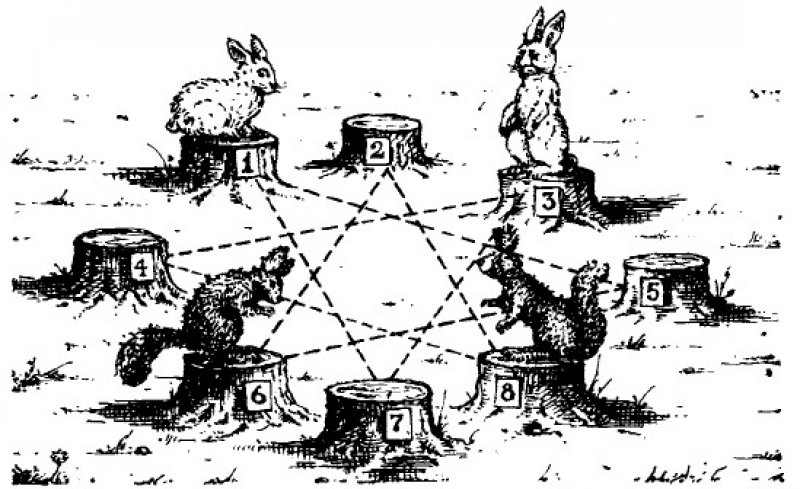
Чтобы оказаться на новом месте, им нужно прыгать с одного пенька на другой по определённым правилам:
1. Прыгать можно только по линиям, которые изображены на рисунке. При этом можно сделать несколько прыжков подряд.
2. На одном пеньке могут находиться только один зверёк, поэтому прыгать нужно только на свободный пенёк.
Кроме того, зверьки хотят поменяться местами за минимальное количество прыжков. Однако им понадобится не меньше 16 прыжков.
Как же они это сделают?
Ответ: Цифры показывают, с какого пня на какой надо прыгать (например, 1–5 означает, что белка прыгает с 1-го пня на 5-й). Всех прыжков понадобится 16, а именно:
1-5;
3 – 7, 7 – 1;
8 – 4, 4 – 3, 3 – 7;
6 – 2, 2 – 8, 8 – 4, 4 – 3;
5 – 6, 6 – 2, 2 – 8;
1 – 5, 5 – 6;
7-1.
1-5;
3 – 7, 7 – 1;
8 – 4, 4 – 3, 3 – 7;
6 – 2, 2 – 8, 8 – 4, 4 – 3;
5 – 6, 6 – 2, 2 – 8;
1 – 5, 5 – 6;
7-1.
Сергей
9 Февраля 2018
Загадка №6784.

Ответ: 447. Нужно посчитать "палочки", из которых состоят числа.
Любитель загадок
9 Января 2020
Три замка и три ключа

Ответ: Достаточно. Обозначим ключи буквами А, В, С, а замки — М, К, Р.
Тогда первая попытка может дать, например, такой результат: ключ А не подходит к замку М. Это означает, что он подходит к замку К или к замку Р.
Вторая попытка: ключ В не подходит к замку М. Тогда ясно, что:
ключ В подходит к замку К или к замку Р;
к замку М подходит ключ С.
Третья попытка ставит всё на свои места: если к замку К не подходит ключ А, то к нему подходит ключ В, а ключ А подходит к замку Р.
Если же с первой попытки выясняется, что ключ А подходит к замку М, то тогда достаточно ещё одной попытки, чтобы установить, какой из оставшихся ключей к какому замку подходит.
Тогда первая попытка может дать, например, такой результат: ключ А не подходит к замку М. Это означает, что он подходит к замку К или к замку Р.
Вторая попытка: ключ В не подходит к замку М. Тогда ясно, что:
ключ В подходит к замку К или к замку Р;
к замку М подходит ключ С.
Третья попытка ставит всё на свои места: если к замку К не подходит ключ А, то к нему подходит ключ В, а ключ А подходит к замку Р.
Если же с первой попытки выясняется, что ключ А подходит к замку М, то тогда достаточно ещё одной попытки, чтобы установить, какой из оставшихся ключей к какому замку подходит.