Место для рекламы
Загадки Якова Исидоровича Перельмана
Яков Исидорович Перельман - загадки
Любитель загадок
19 Ноября 2024
Загадка №9668.
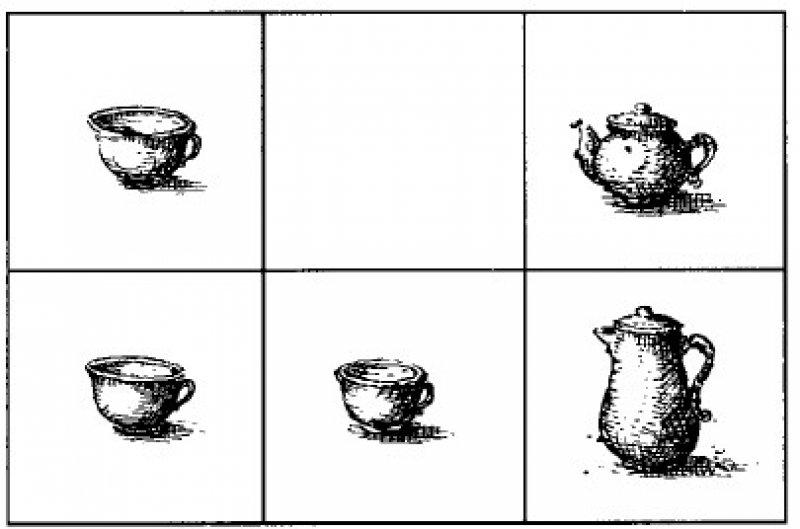
Цель задания — поменять местами чайник и молочник, соблюдая определённые правила:
1. Предмет можно перемещать только в свободную ячейку.
2. Нельзя перемещать предметы по диагонали ячейки.
3. Нельзя ставить один предмет на другой.
4. Нельзя помещать в ячейку более одного предмета, даже временно.
Существует множество решений этой задачи, но интересно найти самое короткое, то есть обменять чайник и молочник за минимальное количество ходов.
Ответ: Для удобства заменим чайную посуду цифрами. Тогда задача представится в таком виде: надо поменять местами предметы 2 и 5.
Вот порядок, в каком их следует передвигать на свободный квадрат:
2, 5, 4, 2,1,3, 2, 4, 5,1,4, 2, 3,4,1,5, 2.
Задача решается в 17 ходов; более короткого решения нет.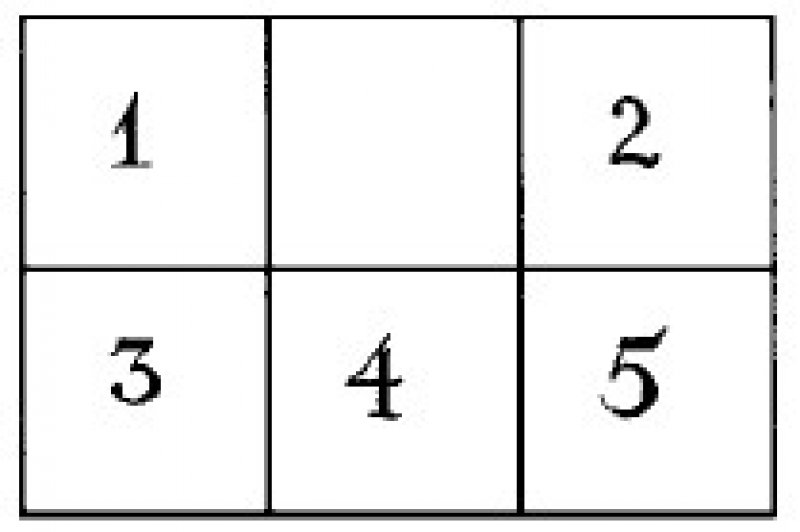
Вот порядок, в каком их следует передвигать на свободный квадрат:
2, 5, 4, 2,1,3, 2, 4, 5,1,4, 2, 3,4,1,5, 2.
Задача решается в 17 ходов; более короткого решения нет.

Любитель загадок
19 Ноября 2024
Белки и кролики
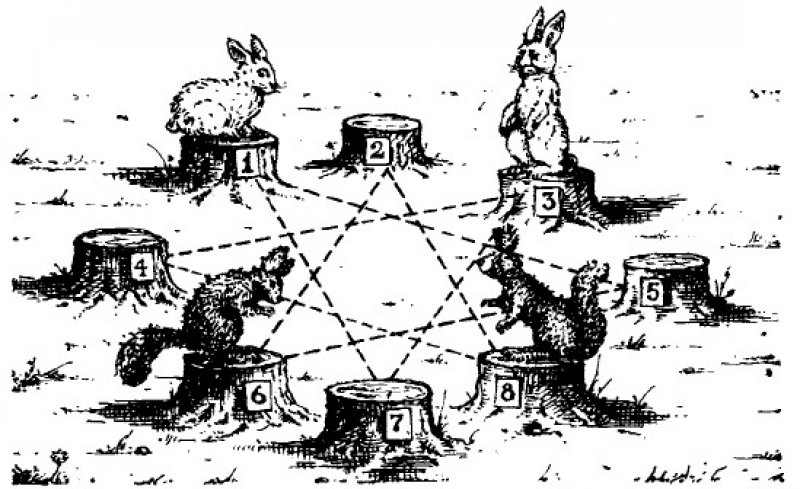
Чтобы оказаться на новом месте, им нужно прыгать с одного пенька на другой по определённым правилам:
1. Прыгать можно только по линиям, которые изображены на рисунке. При этом можно сделать несколько прыжков подряд.
2. На одном пеньке могут находиться только один зверёк, поэтому прыгать нужно только на свободный пенёк.
Кроме того, зверьки хотят поменяться местами за минимальное количество прыжков. Однако им понадобится не меньше 16 прыжков.
Как же они это сделают?
Ответ: Цифры показывают, с какого пня на какой надо прыгать (например, 1–5 означает, что белка прыгает с 1-го пня на 5-й). Всех прыжков понадобится 16, а именно:
1-5;
3 – 7, 7 – 1;
8 – 4, 4 – 3, 3 – 7;
6 – 2, 2 – 8, 8 – 4, 4 – 3;
5 – 6, 6 – 2, 2 – 8;
1 – 5, 5 – 6;
7-1.
1-5;
3 – 7, 7 – 1;
8 – 4, 4 – 3, 3 – 7;
6 – 2, 2 – 8, 8 – 4, 4 – 3;
5 – 6, 6 – 2, 2 – 8;
1 – 5, 5 – 6;
7-1.
Любитель загадок
19 Ноября 2024
Загадка №9669.
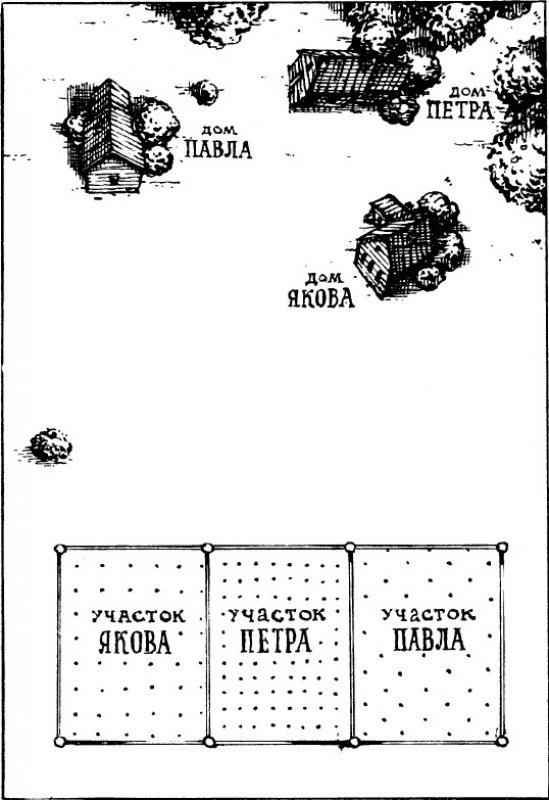
Как видно на рисунке, дома братьев и их земельные участки расположены не совсем удобно. Однако они не могли договориться об обмене участками.
Поскольку кратчайший путь к огородам пересекался, между братьями вскоре начались конфликты, которые переросли в ссоры.
Чтобы прекратить разногласия, братья решили найти такие пути к своим участкам, чтобы не пересекаться друг с другом. После долгих поисков они нашли три таких пути и теперь ежедневно ходят на свои огороды, не встречаясь друг с другом.
Ответ: ответ на рисунке. 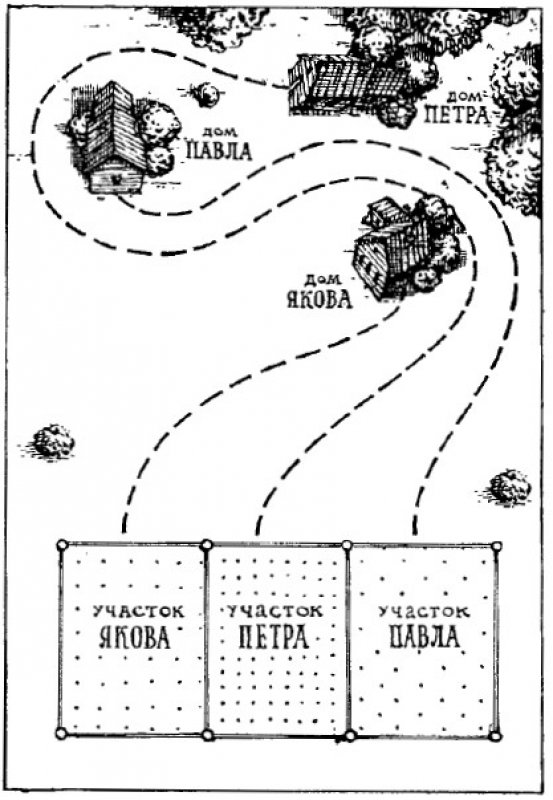

Любитель загадок
5 Декабря 2024
Загадка №9680.
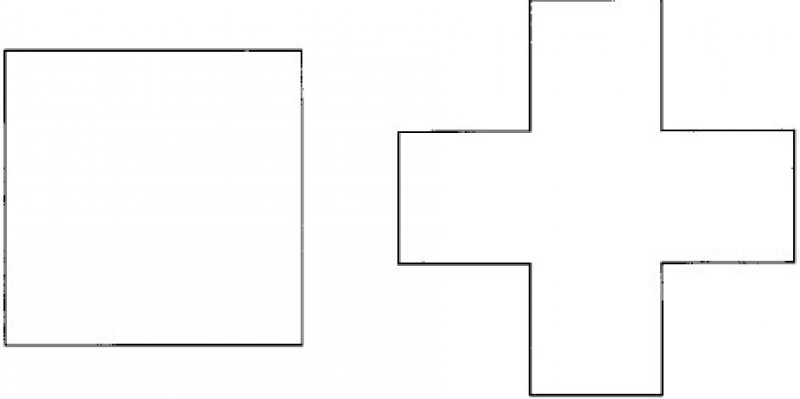
Попробуйте сделать то же самое с квадратным листом бумаги.
Ответ: На картинке 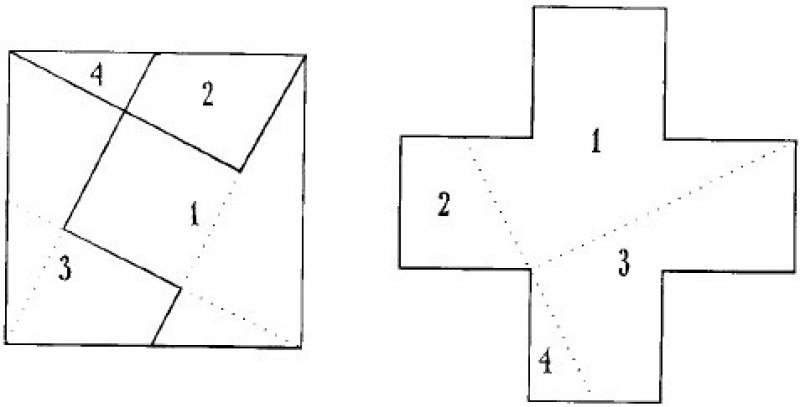

Любитель загадок
22 Ноября 2024
Загадка №9670.
Шесть плотников и столяр нанялись на работу. Плотники заработали по 20 руб., столяр же – на 3 руб. больше, чем заработал в среднем каждый из семерых.Сколько заработал столяр?
Ответ: Легко узнать, каков был средний заработок семерых плотников. Для этого нужно избыточные 3 руб. разделить поровну между 6 плотниками и к 20 руб. каждого прибавить полученные 50 коп. Вычислили средний заработок плотника.
Отсюда узнаем, что столяр заработал
20 руб. 50 коп. + 3 руб., т. е. 23 руб. 50 коп.
Отсюда узнаем, что столяр заработал
20 руб. 50 коп. + 3 руб., т. е. 23 руб. 50 коп.
Любитель загадок
22 Ноября 2024
Девять цифр
Напишите по порядку девять цифр:1 2 3 4 5 6 7 8 9
Вы можете, не меняя расположение цифр, вставить между ними знаки плюс и минус таким образом, чтобы в сумме получилось ровно 100. Нетрудно, например, вставив + и – шесть раз, получить 100 таким путем:
12+ 3–4 + 5 +67+ 8 + 9 = 100
Если хотите вставить + и – только 4 раза, то тоже получите 100:
123 + 4 – 5 + 67 – 89 = 100
Попробуйте, однако, получить 100, пользуясь знаками + и – всего только три раза! Это гораздо труднее. И все же вполне возможно, надо только терпеливо искать решение.
Ответ: 123 – 45 – 67 + 89 = 100
Любитель загадок
27 Ноября 2024
Загадка №9672.
Книга в переплете стоит 2 рубля 50 копеек. Книга на 2 рубля дороже переплета. Сколько стоит переплет?
Ответ: Обычно, не подумав, отвечают: «Переплет стоит 50 копеек». Но ведь тогда книга стоила бы 2 рубля, т. е. была всего на 1 рубль 50 копеек дороже переплета! Верный ответ такой: цена переплета — 25 копеек, цена книги — 2 рубля 25 копеек.
Любитель загадок
27 Ноября 2024
Загадка №9673.
На лугу паслись лошади под присмотром пастухов. Если бы вы пожелали узнать, сколько всех ног на лугу, то насчитали бы 82 ноги. А если бы пересчитали головы, то оказалось бы, что всех голов — лошадиных и человеческих — 26. Сколько на лугу лошадей и сколько пастухов? Надо заметить, что ни безногих лошадей, ни калек-пастухов на лугу не было.
Ответ: Если бы все 26 голов на лугу были человеческие, мы насчитали бы не 82 ноги, а только 52, т. е. на 30 ног меньше. От замены одного человека лошадью число всех ног увеличилось бы на 2. Значит, чтобы насчитать 82 ноги, надо произвести подобную замену 15 раз, тогда и найдутся недостающие 30 ног. Итак, из 26 голов 15 принадлежало лошадям, а остальные 11 — людям.
Любитель загадок
27 Ноября 2024
Дачники и коровы

Ответ: Два варианта решения задачи представлены на рисунке. 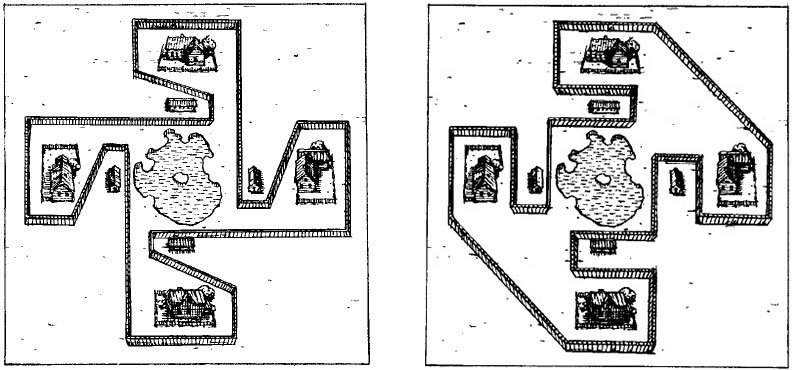

Любитель загадок
27 Ноября 2024
Загадка №9676.

Конечно, эту задачу очень легко решить, если проделать измерения на самом деле. Но попробуйте заранее, без измерения, сказать, какая фигура длиннее, и потом проверьте себя.
Ответ: Это интересный обман зрения: фигура человека, идущего впереди, имеет совершенно такую же длину, как и фигура последнего из идущих. Передний человек кажется нам великаном по сравнению с задним только потому, что изображен вдалеке.
Мы привыкли к тому, что предметы с удалением уменьшаются; поэтому, видя вдали неуменыненную человеческую фигуру, мы невольно заключаем (раз она кажется крупной даже на большом расстоянии), что это – человек исполинских размеров.
Мы привыкли к тому, что предметы с удалением уменьшаются; поэтому, видя вдали неуменыненную человеческую фигуру, мы невольно заключаем (раз она кажется крупной даже на большом расстоянии), что это – человек исполинских размеров.