Место для рекламы
Загадка - «Четырехугольное поле окружено рвом, шири…»
Загадочник
12 Июля 2015
Загадка №3952.
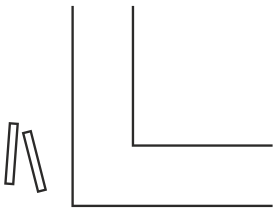
Ответ: Стоит глянуть на приведенный здесь рисунок, что бы понять, как решается задание. Что касается математического доказательства возможности подобной переправы, то он выплывает из неравенства 2√2<3 и делается явным, если принять ширину равную трем каким-либо единицам. 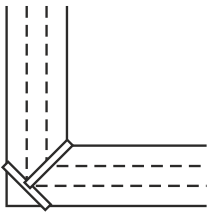

Комментарии
Похожие загадки
Художница
12 Марта 2015
Загадка №3990.
Нам обоим вместе 63 года. В настоящий момент мне лет вдвое больше, чем вам было тогда, когда мне было столько лет, сколько вам в настоящий момент.Сколько мне лет и сколько вам лет?
Ответ: В настоящий момент мне 36, а вам 27. А когда-то мне было 27, а вам 18.
Алексеевич
17 Мая 2015
Загадка №3961.
В Америке дату 1 июля 2003 года записывают так: 7/1/2003, а в других странах: 1/7/2003. Если не знать, в каком формате записанное число, то скольких дат в году можно истолковать неверно?
Ответ: Если есть число 13, можно догадаться что это день, а не месяц. То есть запутаться можно в числах до 12, включая и 12. Всего возможных комбинаций 12x12=144. Но каждый месяц будет иметь одну дату, которая в каждом случае будет понятна правильно, например 7/7/2003. В итоге всего можно истолковать неправильно дней 144-12=132.
Любитель загадок
28 Августа 2015
Загадка №4033.
Эта задача известна с давних времен. Во вьетнамских деревнях старики-рисоводы любят задавать ее молодежи. Так задача переходит от поколения к поколению.Для кормления 100 буйволов заготовили 100 охапок сена.
- Стоящий молодой буйвол съедает 5 охапок сена.
- Лежащий молодой буйвол съедает 3 охапки сена.
- Старые буйволы втроем съедают 1 охапку сена.
Сколько молодых буйволов стоят, сколько лежат и сколько буйволов старых?
Ответ: Пусть х – число стоящих, у – число лежащих молодых буйволов и z – число старых буйволов. Тогда
х + у + z = 100, (1)
5х +3 у + (z/3) = 100, (2)
у = 25 – (7х/4).
Так как х и у – натуральные числа, последнее равенство выполняется только при х = 0, 4, 8, 12. Задача допускает поэтому следующие четыре решения:
x = 0, 4, 8, 12
y = 25, 18, 11, 4
z = 75, 78, 81, 84
х + у + z = 100, (1)
5х +3 у + (z/3) = 100, (2)
у = 25 – (7х/4).
Так как х и у – натуральные числа, последнее равенство выполняется только при х = 0, 4, 8, 12. Задача допускает поэтому следующие четыре решения:
x = 0, 4, 8, 12
y = 25, 18, 11, 4
z = 75, 78, 81, 84
Любитель загадок
28 Сентября 2021
Загадка №9214.
Бабушка принесла на рынок корзинку яблок. Первому своему покупателю она продала половину своих яблок и ещё пол-яблока. Второму — половину от остатка и ещё пол-яблока, третьему — половину от остатка да ещё пол-яблока и так далее.Когда пришел шестой покупатель и купил у неё половину оставшихся яблок и ещё пол-яблока, то оказалось, что бабушка распродала все свои яблоки, и к тому же у всех покупателей яблоки оказались целыми. Сколько яблок бабушка принесла на рынок?
Ответ: Задача решается мгновенно, если сообразить, что последнему шестому покупателю бабушка продала всего одно яблоко. Судите сами: если у неё осталось одно яблоко, то половина от единицы — это половина яблока. Да ещё по-яблока. Итого одно целое яблоко.
Если догадаться до этого, то решение остальной задачи — дело тридцати секунд. Пятый купил 2 яблока, четвертый — 4 яблока, третий — 8 яблок, второй — 16 яблок, первый — 32 яблока. Всего бабушка продала 32+16+8+4+2+1=63 яблока.
А теперь сделаем проверку, чтобы убедиться, что всё в самом деле так.
Первому бабушка продала половину всех яблок и ещё пол-яблока: 63:2+0,5=31,5+0,5=32.
Второму — половину от остатка и ещё пол-яблока: (63-32):2+0,5 = 31:2+0,5 = 15,5+0,5=16.
Если догадаться до этого, то решение остальной задачи — дело тридцати секунд. Пятый купил 2 яблока, четвертый — 4 яблока, третий — 8 яблок, второй — 16 яблок, первый — 32 яблока. Всего бабушка продала 32+16+8+4+2+1=63 яблока.
А теперь сделаем проверку, чтобы убедиться, что всё в самом деле так.
Первому бабушка продала половину всех яблок и ещё пол-яблока: 63:2+0,5=31,5+0,5=32.
Второму — половину от остатка и ещё пол-яблока: (63-32):2+0,5 = 31:2+0,5 = 15,5+0,5=16.
Загадочная
26 Декабря 2015
Загадка №3970.
Дано денег - Один рубль. На эти деньги нужно купить ровно 100 яиц - гусиных, утиных, куриных:- гусиные - по 5 коп./шт;
- утиные - по 3 коп./шт;
- куриные - 1 коп./десяток.
На рубль нужно купить нужно 100 яиц, без сдачи.
Ответ: Гусиных - 16, утиных – 4, куриных - 80.