Место для рекламы
Загадки - Геометрия
Загадки на тему «Геометрия»
Хулиганка
3 Октября 2015
Загадка №3957.
Сколько граней у шестигранного карандаша?
Ответ: 8 граней (6 граней и 2 торцевых).
Люся
26 Января 2016
Загадка №4019.

Ответ: Необходимо сделать поворот на 45 градусов, тогда можно увеличить площадь пруда в два раза, не трогая деревья. 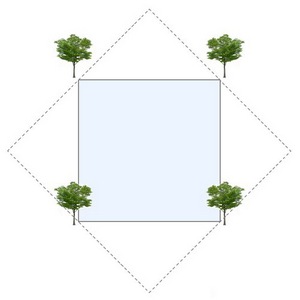

Зиночка
1 Сентября 2015
Загадка для детей №3797.
Ноги очень интересныУ таинственного друга:
Если первая на месте,
То другая ходит кругом!
Ответ: Циркуль
Загадочник
19 Декабря 2015
Загадка для детей №4015.
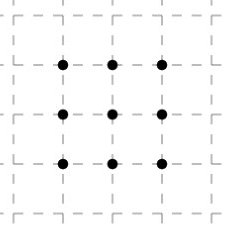
Ответ: Как соединить точки, показано на рисунке. 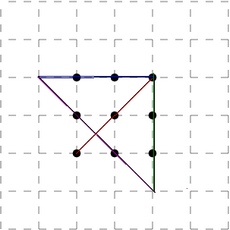

Любитель загадок
10 Марта 2016
Загадка для детей №4107.

Ответ: На картинке 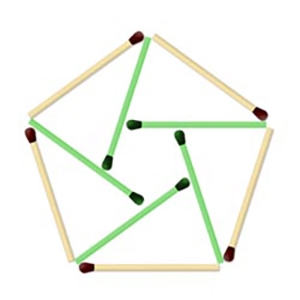

Любитель загадок
31 Января 2016
Загадка для детей №4075.
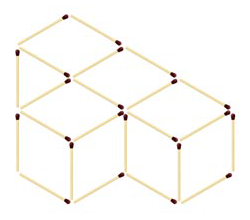
Ответ: на рисунке 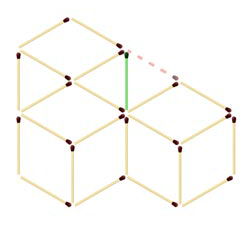

Зиночка
19 Февраля 2015
Загадка для детей №4040.
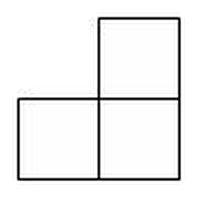
Ответ: Как сделать вырезку видно из рисунка. 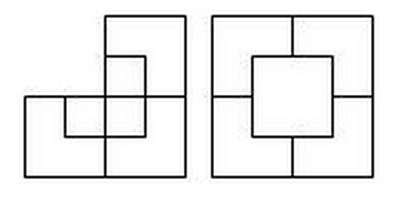

Любитель загадок
31 Января 2015
Загадка для детей №4071.
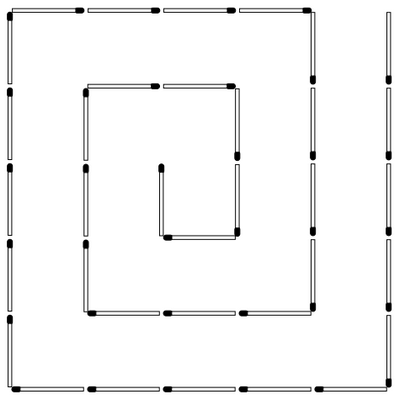
Ответ: на рисунке 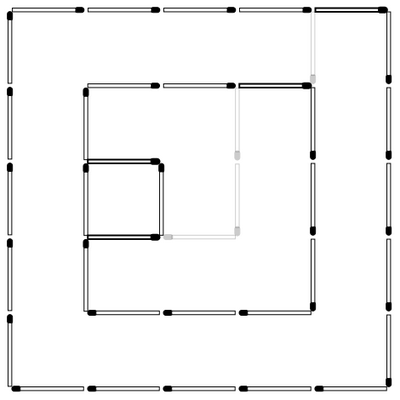

Любитель загадок
18 Апреля 2025
Загадка №9735.
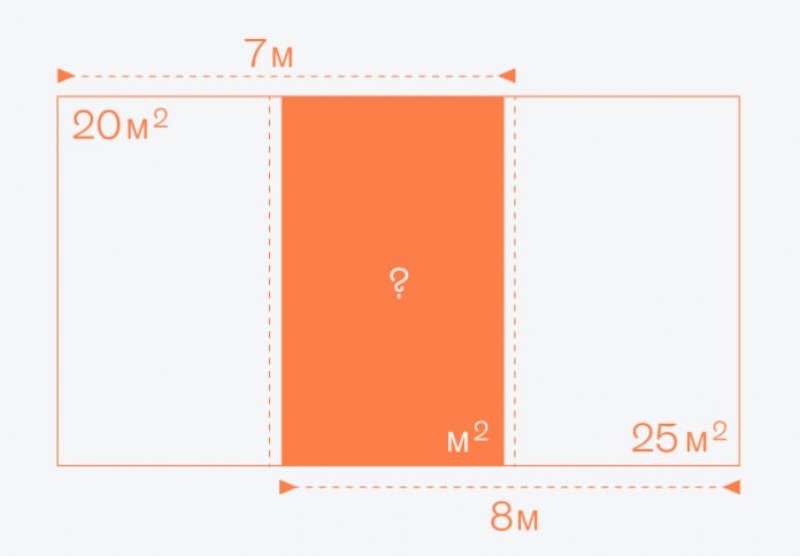
Ответ: Пусть x - длина маленького прямоугольника, а y - ширина прямоугольника.
Тогда:
(8-x)y=25
(7-x)y=20
Решаем уравнения и получаем:
x=3 y=5
S=3×5=15
Тогда:
(8-x)y=25
(7-x)y=20
Решаем уравнения и получаем:
x=3 y=5
S=3×5=15
Любитель загадок
14 Марта 2015
Загадка в рифму №3796.
А братишка мой, Сережа,Математик и чертежник -
На столе у бабы Шуры
Чертит всякие…
Ответ: Фигуры
Алексеевич
4 Августа 2015
Загадка в рифму №3799.
Три вершины тут видны,Три угла, три стороны, -
Ну, пожалуй, и довольно! -
Что ты видишь? - …
Ответ: Треугольник
Валентин
12 Ноября 2015
Загадка в рифму №3795.
Превращать его умеем -Две вершины отведем,
И трапецию имеем!
Не трапецию, так …
Ответ: Ромб
Художница
4 Декабря 2015
Загадка для детей №3801.
Не похож я на пятак,Не похож на рублик.
Круглый я, да не дурак,
С дыркой, но не бублик.
Ответ: Ноль
Сержик
9 Июня 2015
Загадка для детей №3794.
Нет углов у меня,И похож на блюдце я,
На тарелку и на крышку,
На кольцо, на колесо.
Кто же я такой, друзья?
Ответ: Круг
Наталья
24 Сентября 2015
Загадка в рифму №3800.
Эта форма у клубка,У планеты, колобка,
Но сожми ее, дружок,
И получится …
Ответ: Кружок
Художница
7 Декабря 2015
Загадка №3993.
Есть куб — черный снаружи, но белый внутри. Высота его равна его ширине и толщине и составляет три локтя.Задания:
1. Сколько разрезов понадобится, чтобы разделить большой куб на маленькие кубики размером всего в один локоть?
2. Сколько получится кубиков после такого разрезания?
3. Сколько из кубиков будут с 4 черными гранями, сколько — с 3, с 2 и с одной только черной гранью?
4. Сколько всего получится маленьких черных граней и сколько получится кубиков, совершенно белых со всех сторон?
Ответ: 1. Разрезов понадобится всего шесть. Каждую из граней куба надо рассечь дважды.
2. Маленьких кубиков получится 27 штук: три слоя и в каждом — по девять кубиков, выложеных квадратом 3 x 3.
3. Кубиков с четырьмя черными гранями ни одного. С тремя черными гранями окажутся те кубики, которые вырезаны из вершин большого куба. А вершин у куба всего восемь. Чтобы у маленького кубика оказалось только две черные грани, его надо вырезать из середины ребра большого куба. Значит маленьких кубиков с двумя черными гранями получится двенадцать. Ну, и с одной черной гранью получится 6 кубиков.
4. Из каждой большой грани получается 3 x 3 = 9 маленьких. А раз больших граней было шесть, то маленьких выйдет 3 х 3 х 6 = 54. Кубик, у которого все стороны белые, получится только один — из самой середины большого куба.
2. Маленьких кубиков получится 27 штук: три слоя и в каждом — по девять кубиков, выложеных квадратом 3 x 3.
3. Кубиков с четырьмя черными гранями ни одного. С тремя черными гранями окажутся те кубики, которые вырезаны из вершин большого куба. А вершин у куба всего восемь. Чтобы у маленького кубика оказалось только две черные грани, его надо вырезать из середины ребра большого куба. Значит маленьких кубиков с двумя черными гранями получится двенадцать. Ну, и с одной черной гранью получится 6 кубиков.
4. Из каждой большой грани получается 3 x 3 = 9 маленьких. А раз больших граней было шесть, то маленьких выйдет 3 х 3 х 6 = 54. Кубик, у которого все стороны белые, получится только один — из самой середины большого куба.
Любитель загадок
20 Января 2017
Загадка для детей №4616.

Ответ: На картинке 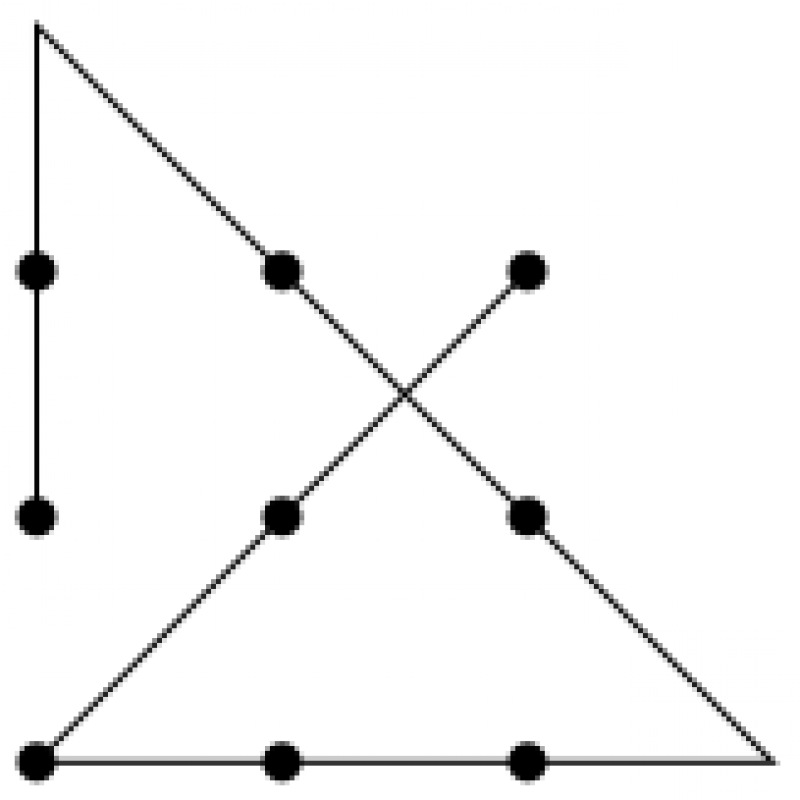

Валентина Калиниченко (Коркина)
27 Января 2017
Загадка для детей №5209.
Что придумал ПифагорМы решаем до сих пор.
Ответ: Теорема
Художница
9 Января 2016
Загадка в рифму №3802.
Едет ручка вдоль листаПо линеечке, по краю -
Получается черта,
Называется …
Ответ: Прямая
Валентина Калиниченко (Коркина)
12 Февраля 2018
Загадка для детей №6787.
Уж такая домоседкаУ двух катетов соседка!
Ответ: Гипотенуза
Зиночка
11 Августа 2015
Загадка для детей №3793.
Он и острый, да не нос,И прямой, да не вопрос,
И тупой он, да не ножик, -
Что еще таким быть может?
Ответ: Угол
Загадочник
12 Июля 2015
Загадка №3952.
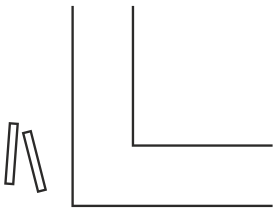
Ответ: Стоит глянуть на приведенный здесь рисунок, что бы понять, как решается задание. Что касается математического доказательства возможности подобной переправы, то он выплывает из неравенства 2√2<3 и делается явным, если принять ширину равную трем каким-либо единицам. 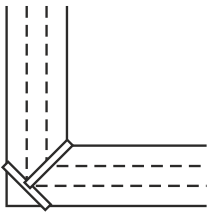

Валентин
7 Октября 2015
Загадка в рифму №3798.
Если взял бы я окружность,С двух сторон немного сжал,
Отвечайте дети дружно -
Получился бы …
Ответ: Овал
Наталья
12 Марта 2015
Загадка в рифму №3790.
Если встали все квадратыНа вершины под углом бы,
То бы видели ребята
Не квадраты мы, а …
Ответ: Ромб
Загадочная
18 Апреля 2015
Загадка в рифму №3791.
Он от солнца прилетает,Пробивая толщу туч
И в тетрадочке бывает,
А зовется просто - …
Ответ: Луч
Загадочная
27 Июня 2015
Загадка в рифму №3792.
Четыре палочки сложилИ вот квадратик получил.
Он давно знаком со мной,
Каждый угол в нем - прямой.
Все четыре стороны
Одинаковой длины.
Вам его представить рад,
А зовут его…
Ответ: Квадрат
Загадочник
14 Июля 2015
Загадка в рифму №3789.
Эта странная фигура,Ну, совсем миниатюра!
И на маленький листочек
Мы поставим сотни …
Ответ: Точек
Люся
9 Июня 2015
Загадка в рифму №3803.
У круга есть одна подруга,Знакома всем ее наружность!
Она идет по краю круга
И называется -…
Ответ: Окружность