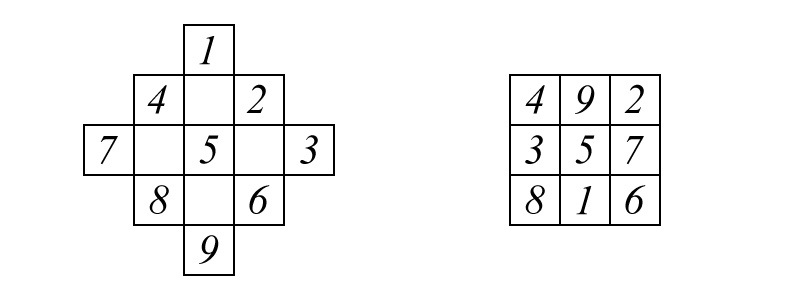Загадка - «Сумма чисел от 1 до 100»
Любитель загадок
28 Января 2017
Сумма чисел от 1 до 100
Клоуну Склеро нужно было сложить все числа от 1 до 100, но после десяти минут напряженной умственной работы Склеро сбился со счета, жалуясь на то, что забыл, каким было последнее прибавленное число...Бедняга не знал, что существует весьма легкий способ решить задачку — на это не потребуется и двадцати секунд! Как это сделать?
Ответ: Сложите самое большое число с самым меньшим, «самое большее минус один» с «самым меньшим плюс один» и так далее (1 + 100 = 101, 2 + 99 = 101, 3 + 98 = 101...); в результате вы получите 50 одинаковых сумм. Следовательно, 101 × 50 = 5050.
Комментарии
Похожие загадки
Любитель загадок
28 Сентября 2021
Загадка №9214.
Бабушка принесла на рынок корзинку яблок. Первому своему покупателю она продала половину своих яблок и ещё пол-яблока. Второму — половину от остатка и ещё пол-яблока, третьему — половину от остатка да ещё пол-яблока и так далее.Когда пришел шестой покупатель и купил у неё половину оставшихся яблок и ещё пол-яблока, то оказалось, что бабушка распродала все свои яблоки, и к тому же у всех покупателей яблоки оказались целыми. Сколько яблок бабушка принесла на рынок?
Ответ: Задача решается мгновенно, если сообразить, что последнему шестому покупателю бабушка продала всего одно яблоко. Судите сами: если у неё осталось одно яблоко, то половина от единицы — это половина яблока. Да ещё по-яблока. Итого одно целое яблоко.
Если догадаться до этого, то решение остальной задачи — дело тридцати секунд. Пятый купил 2 яблока, четвертый — 4 яблока, третий — 8 яблок, второй — 16 яблок, первый — 32 яблока. Всего бабушка продала 32+16+8+4+2+1=63 яблока.
А теперь сделаем проверку, чтобы убедиться, что всё в самом деле так.
Первому бабушка продала половину всех яблок и ещё пол-яблока: 63:2+0,5=31,5+0,5=32.
Второму — половину от остатка и ещё пол-яблока: (63-32):2+0,5 = 31:2+0,5 = 15,5+0,5=16.
Если догадаться до этого, то решение остальной задачи — дело тридцати секунд. Пятый купил 2 яблока, четвертый — 4 яблока, третий — 8 яблок, второй — 16 яблок, первый — 32 яблока. Всего бабушка продала 32+16+8+4+2+1=63 яблока.
А теперь сделаем проверку, чтобы убедиться, что всё в самом деле так.
Первому бабушка продала половину всех яблок и ещё пол-яблока: 63:2+0,5=31,5+0,5=32.
Второму — половину от остатка и ещё пол-яблока: (63-32):2+0,5 = 31:2+0,5 = 15,5+0,5=16.
Сергей
8 Февраля 2018
Загадка №6782.
У женщины спросили: "Сколько Вам лет?". Она ответила: "30, не считая суббот и воскресений". Сколько ей лет?
Ответ: Женщине 42 года.
Решение. Без суббот и воскресений - значит считать каждые 5 дней в неделю, т.е. лишь 5/7 жизни. Если 5/7 это 30 лет, то верный ответ 30 × 7 / 5 = 42.
Решение. Без суббот и воскресений - значит считать каждые 5 дней в неделю, т.е. лишь 5/7 жизни. Если 5/7 это 30 лет, то верный ответ 30 × 7 / 5 = 42.
Mr. Goodcat
17 Мая 2017
Помогите решить.
Ответ: 90,5 кг. Решение в комментариях.
Художница
17 Января 2016
Загадка №3976.
Летела стая гусей, увидел их дядька и говорит:– По-видимому, вас сто!
А гуси и отвечают:
– «Если бы нас столько,
Да еще бы столько,
И половину как столько,
И четверть как столько,
И ты бы с нами, – тогда бы сто и было».
Сколько гусей?
Ответ: 36 гусей: 36+36+18+9+1=100.
Любитель загадок
22 Января 2017
Загадка №4731.
Ответ: Для решения этой задачи можно воспользоваться одним легко запоминающимся приёмом. Сперва расставим числа так, как показано на рисунке.
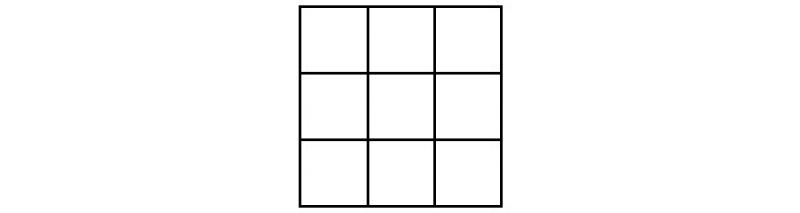
Теперь сдвинем стоящие вне квадрата числа соответственно на 3 клетки влево, вправо, вниз и вверх так, чтобы они попали на свободные места в квадрате. Получим нужное размещение.
Этот способ пригоден для построения волшебных квадратов с любым нечётным количеством клеток.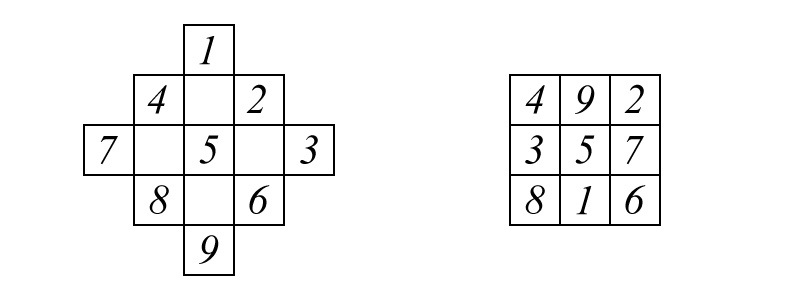
Теперь сдвинем стоящие вне квадрата числа соответственно на 3 клетки влево, вправо, вниз и вверх так, чтобы они попали на свободные места в квадрате. Получим нужное размещение.
Этот способ пригоден для построения волшебных квадратов с любым нечётным количеством клеток.
