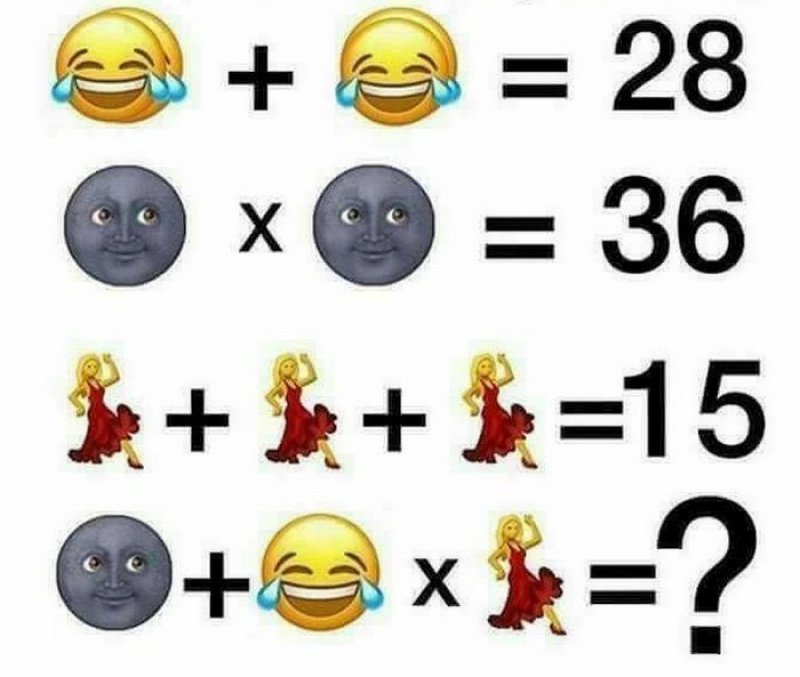Место для рекламы
Новые загадки - На логику (Страница 2)
На логику - новые загадки
Любитель загадок
15 Февраля 2024
Загадка №9343.

Ответ: Седьмая вода на киселе
Любитель загадок
8 Декабря 2023
Загадка №9337.

Ответ: Курс (Корабль держит курс, курс лекций, курс валют)
Любитель загадок
6 Декабря 2023
Загадка №9325.

Ответ: Песня «Кондуктор, нажми на тормоза», из фильма «Операция Ы и другие приключения Шурика».
Любитель загадок
27 Апреля 2022
Загадка №9255.
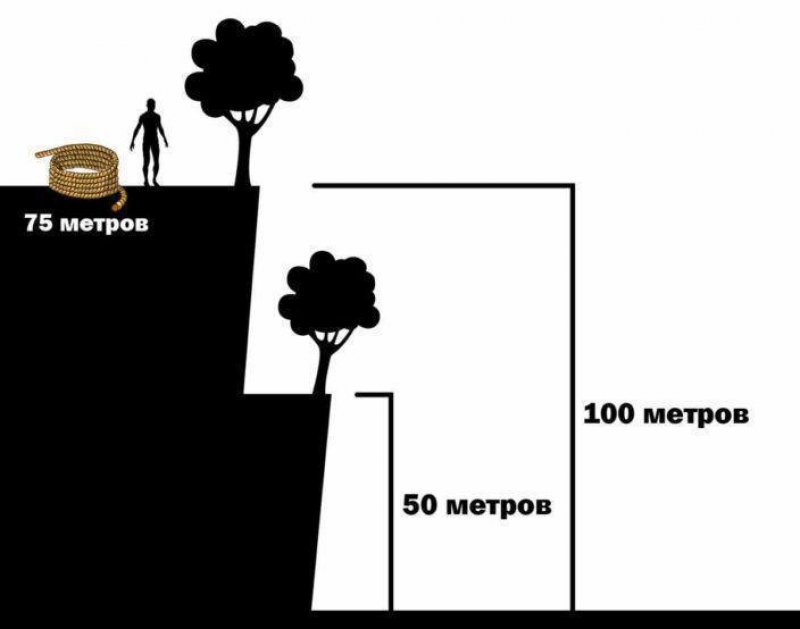
Ответ: Главная проблема альпиниста в том, что если он привяжет верёвку к первому дереву и спустится до второго, то он уже не сможет подняться и развязать верёвку, чтобы хватило на второй спуск. Поэтому ему нужно действовать так:
1 Отмерить и отрезать кусок в 25 метров (например, спустив один конец верёвки, чтобы он коснулся дерева, сколько останется — это и есть 25 метров).
2 Один конец 25-метровой верёвки привязать к первому дереву, а на конце второго сделать маленькую петлю.
3 Пропустить оставшуюся 50-метровую верёвку в эту петлю и сложить пополам. Общая длина этой конструкции получится как раз 25 + 25 = 50 метров.
4 На этой связке спуститься до второго дерева, держась за оба конца сложенной 50-метровой верёвки.
5 Отпустить один конец, потянуть за второй и вытащить всю 50-метровую верёвку через петлю, где она держалась.
6 На этой верёвке спокойно спуститься до земли.
1 Отмерить и отрезать кусок в 25 метров (например, спустив один конец верёвки, чтобы он коснулся дерева, сколько останется — это и есть 25 метров).
2 Один конец 25-метровой верёвки привязать к первому дереву, а на конце второго сделать маленькую петлю.
3 Пропустить оставшуюся 50-метровую верёвку в эту петлю и сложить пополам. Общая длина этой конструкции получится как раз 25 + 25 = 50 метров.
4 На этой связке спуститься до второго дерева, держась за оба конца сложенной 50-метровой верёвки.
5 Отпустить один конец, потянуть за второй и вытащить всю 50-метровую верёвку через петлю, где она держалась.
6 На этой верёвке спокойно спуститься до земли.
Любитель загадок
11 Апреля 2022
Загадка №9251.
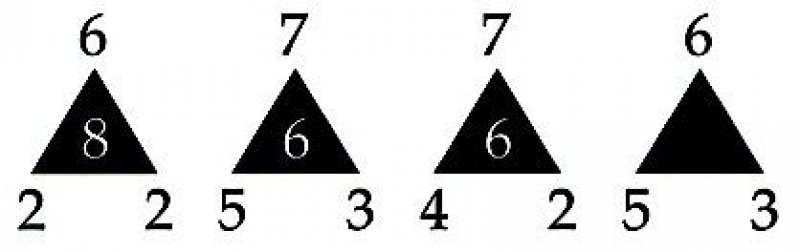
Ответ: Ответ: число 3. Правила для каждого треугольника выглядит следующим образом: берёте верхнее число, вычитаете из него нижнее левое и умножаете ответ на цифру в нижнем правом углу.
Любитель загадок
9 Марта 2022
Загадка про 4 таблетки

Взяв у врача таблетки, пациент по своей неосторожности смешал их между собой, и, спустя некоторое время, к своему ужасу обнаружил, что таблетки противоядия и катализатора абсолютно неразличимы между собой.
Для того, чтобы гарантированно выжить, умирающему было предписано выпить лекарство в два приёма с перерывом в несколько часов, каждый раз принимая противоядие только с его катализатором.
Приём четырёх таблеток за один приём грозил смертью от передозировки; приём двух таблеток противоядия без катализатора не произвёл бы никакого действия....
Как путешественнику выжить в сложившейся ситуации?
Ответ: Нужно разделить все таблетки на две части и выпить по половинке от каждой в первый прием, а оставшиеся во второй прием.
Любитель загадок
28 Сентября 2021
Загадка №9214.
Бабушка принесла на рынок корзинку яблок. Первому своему покупателю она продала половину своих яблок и ещё пол-яблока. Второму — половину от остатка и ещё пол-яблока, третьему — половину от остатка да ещё пол-яблока и так далее.Когда пришел шестой покупатель и купил у неё половину оставшихся яблок и ещё пол-яблока, то оказалось, что бабушка распродала все свои яблоки, и к тому же у всех покупателей яблоки оказались целыми. Сколько яблок бабушка принесла на рынок?
Ответ: Задача решается мгновенно, если сообразить, что последнему шестому покупателю бабушка продала всего одно яблоко. Судите сами: если у неё осталось одно яблоко, то половина от единицы — это половина яблока. Да ещё по-яблока. Итого одно целое яблоко.
Если догадаться до этого, то решение остальной задачи — дело тридцати секунд. Пятый купил 2 яблока, четвертый — 4 яблока, третий — 8 яблок, второй — 16 яблок, первый — 32 яблока. Всего бабушка продала 32+16+8+4+2+1=63 яблока.
А теперь сделаем проверку, чтобы убедиться, что всё в самом деле так.
Первому бабушка продала половину всех яблок и ещё пол-яблока: 63:2+0,5=31,5+0,5=32.
Второму — половину от остатка и ещё пол-яблока: (63-32):2+0,5 = 31:2+0,5 = 15,5+0,5=16.
Если догадаться до этого, то решение остальной задачи — дело тридцати секунд. Пятый купил 2 яблока, четвертый — 4 яблока, третий — 8 яблок, второй — 16 яблок, первый — 32 яблока. Всего бабушка продала 32+16+8+4+2+1=63 яблока.
А теперь сделаем проверку, чтобы убедиться, что всё в самом деле так.
Первому бабушка продала половину всех яблок и ещё пол-яблока: 63:2+0,5=31,5+0,5=32.
Второму — половину от остатка и ещё пол-яблока: (63-32):2+0,5 = 31:2+0,5 = 15,5+0,5=16.
Любитель загадок
9 Сентября 2021
Загадка №9200.

Ответ: 1) Идут в разных направлениях домой, значит из школы, если смотреть на часы, учатся во вторую смену или занимались на продленки, т.к. с утра до 5 часов не учатся.
2) В больницу, из больнице домой в белой простыне отвозят только в последний путь.
3) Почтальон отработал, время 5 часов, сумка пустая.
4) Понятно что из детсада, время 5 ч. и на заднем плане написано Детсад.
5) Человек приехал домой, его радостно встречают.
6) Дождя не было, если-бы был, то дворник со шлангом не возился, ветер дует справа.
7) Осень, сентябрь - арбузы, школьники.
2) В больницу, из больнице домой в белой простыне отвозят только в последний путь.
3) Почтальон отработал, время 5 часов, сумка пустая.
4) Понятно что из детсада, время 5 ч. и на заднем плане написано Детсад.
5) Человек приехал домой, его радостно встречают.
6) Дождя не было, если-бы был, то дворник со шлангом не возился, ветер дует справа.
7) Осень, сентябрь - арбузы, школьники.
Любитель загадок
15 Февраля 2021
Загадка №8520.

Ответ: Знаки зодиака (Близнецы, Лев, Водолей)
Любитель загадок
10 Февраля 2021
Загадка №8515.

Однажды подруги Ася, Ира, Клава и Женя отправились за покупками, причем каждой был нужен только один свой магазин. По дороге они обменивались такими замечаниями.
Ася: «Женя и я хотели пойти вместе ещё раньше на этой неделе, но не было такого дня, чтобы мы обе могли сделать наши покупки».
Ира: «Я не хотела идти сегодня, но завтра я уже не смогу купить то, что мне нужно».
Клава: «А я могла бы пойти в магазин и вчера, и позавчера».
Женя: «А я могла бы пойти и вчера, и завтра».
Скажите, кому какой магазин нужен?
Ответ: Ася в хозяйственный, Ира в парфюмерный, Клава в продовольственный, Женя в обувной.
Любитель загадок
23 Января 2021
Загадка №8379.

Ответ: Пусть до полуночи Х часов.
Тогда, составляем уравнение:
Х+2=(Х+1)/2.
2Х+4=Х+1;
Х=-3.
То есть сейчас три часа до полуночи, а это девять часов вечера или 21:00.
Тогда, составляем уравнение:
Х+2=(Х+1)/2.
2Х+4=Х+1;
Х=-3.
То есть сейчас три часа до полуночи, а это девять часов вечера или 21:00.
Любитель загадок
20 Января 2021
Загадка №8366.

Ответ: Круглый ("Круглая" земля, круглый отличник, круглая дата)
Любитель загадок
19 Января 2021
Загадка №8355.

Ответ: Ответ на картинке. 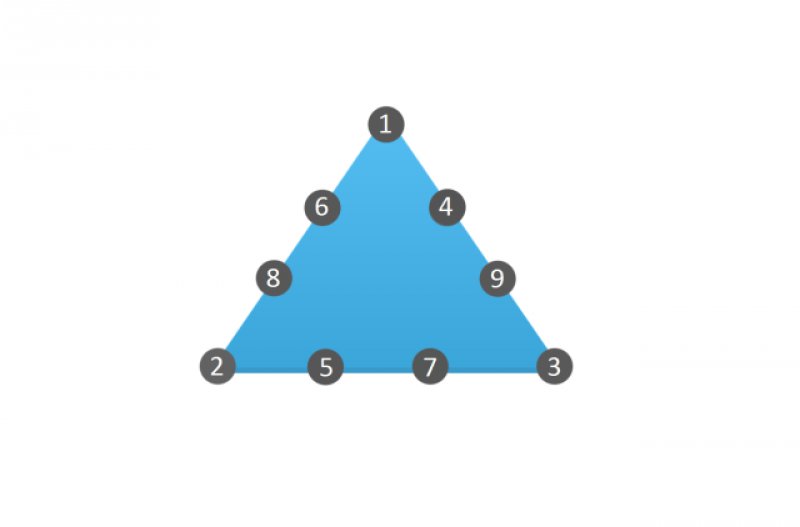

Загадочник логики
8 Ноября 2020
Загадка №8298.
На огороде за 1 день вырастает 3 картошки, каждый 3 день фермер собирает с огорода 3 картошки. На 6 дней сколько фермер соберет всего картошки?
Ответ: 15 картошек.
Иван Набатов
21 Октября 2020
Загадка №8297.
летели птицы, одна впереди две сзади, две впереди одна сзади, и три в ряд! сколько летело птиц???
Ответ: 3 птицы. Потому что одно впереди а две зади сколько три ,просто потом они меняли свои позиции то вряд, то одно зади две впереди.
LenoryakYT
31 Марта 2020
Загадка №8231.
Построили многоэтажный дом. На 12 этаже живёт 11 человек, на 1 этаже 2 человека, а на остальных по 5 человек. Через неделю одна из кнопок лифта стёрлась, какая?
Ответ: Кнопка 1-го этажа, ведь на первый этаж ездили со всех этажей.
Любитель загадок
15 Февраля 2020
Загадка для детей №8208.

Ответ: Табличку Б. Сумма чисел в каждом из столбцов табличек соответственно равна: 13, 14, 15.
Любитель загадок
9 Января 2020
Три замка и три ключа

Ответ: Достаточно. Обозначим ключи буквами А, В, С, а замки — М, К, Р.
Тогда первая попытка может дать, например, такой результат: ключ А не подходит к замку М. Это означает, что он подходит к замку К или к замку Р.
Вторая попытка: ключ В не подходит к замку М. Тогда ясно, что:
ключ В подходит к замку К или к замку Р;
к замку М подходит ключ С.
Третья попытка ставит всё на свои места: если к замку К не подходит ключ А, то к нему подходит ключ В, а ключ А подходит к замку Р.
Если же с первой попытки выясняется, что ключ А подходит к замку М, то тогда достаточно ещё одной попытки, чтобы установить, какой из оставшихся ключей к какому замку подходит.
Тогда первая попытка может дать, например, такой результат: ключ А не подходит к замку М. Это означает, что он подходит к замку К или к замку Р.
Вторая попытка: ключ В не подходит к замку М. Тогда ясно, что:
ключ В подходит к замку К или к замку Р;
к замку М подходит ключ С.
Третья попытка ставит всё на свои места: если к замку К не подходит ключ А, то к нему подходит ключ В, а ключ А подходит к замку Р.
Если же с первой попытки выясняется, что ключ А подходит к замку М, то тогда достаточно ещё одной попытки, чтобы установить, какой из оставшихся ключей к какому замку подходит.
Любитель загадок
31 Октября 2019
Ведьмы, вампиры и оборотни

Всего было 100 вампиров, 99 оборотней и 101 ведьма. Древнее заклинание, наложенное на всех, запрещает убивать тех, кто погубил нечетное число жертв. В настоящее время в лесу остался всего 1 житель.
Кто это и почему?
Ответ: Все 300 обитателей леса делятся на 3 группы:
1) оставшийся в живых (1 шт)
2) убитые им (они все одного вида)
3) убитые убитыми (чётное количество в каждом виде)
Отсюда ясно, что пункты 1 и 2 принадлежат видам с нечётной численностью. Если бы в живых остался 1 оборотень, то умерло бы 100 вампиров, 98 оборотней, 101 ведьма. Каждый умерший вампир убил четное число ведьм, но ведьм умерло нечетное число - противоречие. Следовательно, в живых осталась 1 ведьма.
1) оставшийся в живых (1 шт)
2) убитые им (они все одного вида)
3) убитые убитыми (чётное количество в каждом виде)
Отсюда ясно, что пункты 1 и 2 принадлежат видам с нечётной численностью. Если бы в живых остался 1 оборотень, то умерло бы 100 вампиров, 98 оборотней, 101 ведьма. Каждый умерший вампир убил четное число ведьм, но ведьм умерло нечетное число - противоречие. Следовательно, в живых осталась 1 ведьма.
Любитель загадок
17 Сентября 2019
Загадка №8099.

Ответ подскажут болельщики одной и той же команды. Разберитесь в их футбольных симпатиях.
Ответ: Было две команды болельщиков: в первую входили болельщики на местах 1,5,6,7 во вторую команду входили болельщики на местах 2,3,4,8. Победила команда за которую болели болельщики на местах 1,5,6,7.. Счет 5:3!!!!
Любитель загадок
17 Сентября 2019
Загадка для детей №8098.

Ответ: По условию задачи ясно, что ни одного из двух мальчиков, между которыми стоит Нюра, не зовут Володей; чтобы оказаться рядом с Володей, девочке, очевидно, надо стать на второе место слева. Тогда справа оказались бы по соседству друг с другом два тезки. Значит, крайний слева Коля, за ним Володя, дальше Петя, Нюра и второй Петя.
Dievsky
30 Августа 2019
Загадка про шары (помогите решить)
Есть помещение, в нем 100 шаров. Внутри каждого из шаров цифра от 1 до 100. Шары перемешаны.Задача:
В данное помещение по очереди заходят два человека.
Первый может зайти и посмотреть все шары. Открыть и посмотреть какая в каждом из шаров спрятана цифра.
Так же у него есть возможность взять два произвольных шара и положить их в любое место в ряду из 100 шаров.
После чего он выходит из комнаты через другую дверь, так как ему никоим образом не разрешено контактировать со вторым человеком, его товарищем.
Затем заходит в комнату второй человек.
Ему говорят: - мы щас тебе задаем число от 1 до 100, и ты должен за 50 попыток найти в каком шару это число, если ты не найдешь, то мы тебя с другом убьем!
Однако, эти оба знали, что им будет предстоять такая задача, и они заранее о чем-то договорились, придумали какой-то хитрый алгоритм, который в итоге спас им жизни.
Как же второму удалось вычислить где шар с нужным числом?
Ответ: ответ пока неизвестен
Любитель загадок
7 Июня 2019
Загадка №8056.

В 1-й коробке числа: 6, 0, 8, 3, 9;
Во 2-й коробке: 1, 7, 11, 4, 14;
В 3-й коробке: 2, 12, 5, 10, 13.
Ваша задача состоит в том, чтобы понять этот принцип и поместить следующие три числа - 15, 16, 17 - в нужные коробки.
Ответ: Числа 15 и 16 должны оказаться в коробке 3, а число 17 в коробке 2. Числа в коробке 1 все вычерчены с использованием только кривых линий. Числа в коробке 2 - с использованием только прямых линий. В начертаниях чисел, собранных в коробке 3, есть как прямые, так и кривые линии.
Любитель загадок
10 Апреля 2019
Шарики в коробочках
Перед Вами пять коробочек: белая, черная, красная, синяя и зелёная. Также есть по два шарика для каждого из цветов. В каждой коробочке лежит по два шарика, причём цвета коробочки и шариков могут не совпадать. Также известно, что:1. Ни один шарик не лежит в коробочке того же цвета, что и он сам;
2. В красной коробочке нет синих шариков;
3. В коробочке нейтрального цвета (то есть белого или чёрного) лежит один красный и один зелёный шарик;
4. В чёрной коробочке лежат шарики холодных тонов (зелёный и синий цвета);
5. В одной из коробочек лежат один белый и один синий шарик;
6. В синей коробочки находится один чёрный шарик.
Какого цвета шарики лежат в каждой коробочке?
Ответ: Белая коробочка - красный и зеленый;
черная коробочка - зеленый и синий;
зеленая коробочка - белый и синий;
синяя коробочка- черный и красный;
красная коробочка - белый и черный.
черная коробочка - зеленый и синий;
зеленая коробочка - белый и синий;
синяя коробочка- черный и красный;
красная коробочка - белый и черный.
Любитель загадок
3 Апреля 2019
Рыцари и лжецы 3
В этой задаче два персонажа: А и В. Каждый из них либо рыцарь, либо лжец. А высказывает следующее утверждение: "По крайней мере один из нас лжец". Кто из двух персонажей А и В рыцарь и кто лжец?
Ответ: Предположим, что А - лжец. Если бы это было так, то утвержденне "По крайней мере одни из нас лжец" было бы ложным (так как лжецы высказывают ложные утверждения). Следовательно, в этом случае А н В были бы рыцарями. Таким образом, если бы А был лжецом, то он не был бы лжецом, что невозможно. Отсюда мы заключаем, что А не лжец, он рыцарь. Но тогда высказанное А утверждение должно быть истинным. Поэтому по крайней мере один из двух персонажей А и В в действительности лжей. Так как А - рыцарь, то лжецом должен быть В. Итак, А - рыцарь, а В - лжец.
Загадки на связанные темы:
Автобус Антифразы В картинках Вероятность Внимательность Геометрия Головоломки Деньги Детективные Дни недели Загадки Старца Фура Карты игральные Кровать легкая Монеты Найди общее Одежда Париж Последовательности Расстановки Родственники С шашками Смекалка Со спичками Советские Угадай песню Угадай фразеологизм Хеллоуин Числа Числовые ребусы Шахматы Шерлок Холмс Шифр Эрудиция