Место для рекламы
Новые загадки - Математические (Страница 4)
Математические - новые загадки
Хулиганка
2 Декабря 2015
Загадка для детей №3740.
Сколько будет 2+2х2=?
Ответ: 6 (первое действие умножение)
Хулиганка
28 Ноября 2015
Загадка №3966.
Перед вами выражение 987654321=100. Сделайте его верным, используя 4 знака "+" или "-" в его левой части.
Ответ: 98 - 76 + 54 + 3 + 21 = 100
Художница
26 Ноября 2015
Загадка №2246.
В каком числе цифр столько, сколько букв в его названии?
Ответ: 100 (сто), 1000000 (миллион)
Загадочная
22 Ноября 2015
Загадка с подвохом №2279.
Марина мечтала о шоколадке, но ей на покупку не хватало 10 рублей. Вася тоже мечтал о шоколадке, но ему не доставало всего 1 рубля. Дети решили купить хотя бы одну шоколадку на двоих, но им все равно не хватило 1 рубля. Какова стоимость шоколадки?
Ответ: Стоимость - 10 рублей. У Марины нет денег вообще
Валентин
9 Ноября 2015
Загадка №3955.
В зоомагазине продают больших и маленьких птиц. Большая птица вдвое дороже маленькой. Леди, которая зашла в магазин, купила 5 больших птиц и 3 маленьких. Если бы она вместо этого купила 3 больших птицы и 5 маленьких, то потратила бы на 20 долларов меньше. Сколько стоит каждая птица?
Ответ: Цена большой птицы 20 долларов, а маленькой — 10 долларов. Решение: пусть цена маленькой птицы будет x, тогда большой будет y=2x. Леди купила 5 больших и три маленьких, то есть 5y + 3x. Если бы она купила 3 больших и пять маленьких, то есть 3y + 5x, то витратила б на 20 то потратила бы на 20 долларов меньше. Получаем: (5y + 3x) - (3y + 5x) = 20 -> 2y - 2x = 20 -> 4x - 2x = 20 -> x = 10 -> y = 2x = 20.
Сержик
1 Ноября 2015
Загадка с подвохом №3733.
Как правильно? Пять плюс семь будет «одиннадцать» или «адиннадцать»?
Ответ: Двенадцать
Загадочник
21 Октября 2015
Загадка №4003.
Дерево отбрасывает тень длиной 10 м. Столб длиной 3 м отбрасывает тень длиной 2 м. Чему равняется высота дерева?
Ответ: Высота дерева относится к длине тени, что оно отбрасывает, так же, как высота столба к длине своей тени, значит
х : 10 = 3 : 2
х =15.
Отсюда, высота дерева равняется 15 м.
х : 10 = 3 : 2
х =15.
Отсюда, высота дерева равняется 15 м.
Зиночка
17 Октября 2015
Загадка №3978.
Стрелки часов только что совпали. Через сколько минут они будут «смотреть» в противоположные стороны?
Ответ: Пусть х - промежуток времени (в минутах), которое должно пройти прежде, чем стрелки расположатся на одной прямой и будут направлены в противоположные стороны. Минутная стрелка успеет пройти за это время х минутных делений циферблата, а часовая - х/12 минутных делений. Когда стрелки расположатся на одной прямой и будут направлены в противоположные стороны, их будут разделять 30 минутных делений циферблата.
Следовательно, в это время:
x – x/12 = 30,
откуда х = 32 (8/11).
Через 32 (8/11) мин. после того, как минутная и часовая стрелки совпадут, они будут «смотреть» в противоположные стороны.
Следовательно, в это время:
x – x/12 = 30,
откуда х = 32 (8/11).
Через 32 (8/11) мин. после того, как минутная и часовая стрелки совпадут, они будут «смотреть» в противоположные стороны.
Админ
16 Октября 2015
Загадка №4000.
Это не столько загадка, сколько фокус, основанный на математике. Попросите кого-нибудь задумать (написать, чтобы вы не видели) пятизначное число, потом умножить его на девять и зачеркнуть любую цифру. А теперь попросите сложить оставшиеся цифры и назвать сумму. После чего вы без труда угадаете зачеркнутую цифру.
Ответ: В основе фокуса лежит правило - что если число делиться на 9, то и его сумма делится на 9. Когда вычеркивают цифру то сумма становится не кратна 9 и вам надо найти ближайшее число кратное девяти. Разница между названной суммой и этим числом и будет вычеркнутое число.
Админ
13 Сентября 2015
Загадка №4029.
Как измерить диаметр тонкой проволоки, имея в распоряжении лишь карандаш и масштабную линейку?
Ответ: Необходимо плотно обмотать (виток к витку) проволокой карандаш измерте длинну обмотки. Полученную цифру разделите на количество витков.
Люся
9 Сентября 2015
Загадка с подвохом №3774.
Одна яхта идет из Ниццы в Сан-Ремо, другая - из Сан-Ремо в Ниццу. Из гаваней они вышли одновременно. Первый час движения яхты шли с одинаковой скоростью (60 км/ч), но потом первая яхта увеличила скорость до 80 км/ч. Какая из яхт будет ближе к Ницце в момент их встречи?
Ответ: В момент встречи они будут на одинаковом расстоянии от Ниццы
Наталья
5 Сентября 2015
Загадка с подвохом №2195.
На столе лежит 100 листов бумаги. За каждые 10 секунд можно посчитать 10 листов. Сколько секунд понадобится, чтобы посчитать 80 листов?
Ответ: 20 (Отсчитать 20 листов, останется 80)
Любитель загадок
28 Августа 2015
Загадка №4033.
Эта задача известна с давних времен. Во вьетнамских деревнях старики-рисоводы любят задавать ее молодежи. Так задача переходит от поколения к поколению.Для кормления 100 буйволов заготовили 100 охапок сена.
- Стоящий молодой буйвол съедает 5 охапок сена.
- Лежащий молодой буйвол съедает 3 охапки сена.
- Старые буйволы втроем съедают 1 охапку сена.
Сколько молодых буйволов стоят, сколько лежат и сколько буйволов старых?
Ответ: Пусть х – число стоящих, у – число лежащих молодых буйволов и z – число старых буйволов. Тогда
х + у + z = 100, (1)
5х +3 у + (z/3) = 100, (2)
у = 25 – (7х/4).
Так как х и у – натуральные числа, последнее равенство выполняется только при х = 0, 4, 8, 12. Задача допускает поэтому следующие четыре решения:
x = 0, 4, 8, 12
y = 25, 18, 11, 4
z = 75, 78, 81, 84
х + у + z = 100, (1)
5х +3 у + (z/3) = 100, (2)
у = 25 – (7х/4).
Так как х и у – натуральные числа, последнее равенство выполняется только при х = 0, 4, 8, 12. Задача допускает поэтому следующие четыре решения:
x = 0, 4, 8, 12
y = 25, 18, 11, 4
z = 75, 78, 81, 84
Валентин
23 Августа 2015
Загадка №4008.
Одна женщина отправилась в сад собирать яблоки. Чтобы выйти из сада, ей нужно было пройти через четверо дверей, у каждой из которых стоял стражник. Стражнику у первых дверей женщина отдала половину сорванных ею яблок. Дойдя до второго стражника, женщина отдала ему половину яблок, которые остались. Так же она сделала и с третьим стражником; а когда она поделилась яблоками со стражником у четвертых дверей (с которым она сделали как и с предыдущими) то у нее осталось лишь 10 яблок. Сколько яблок она собрала в саду?
Ответ: Если х - число яблок, собранных женщиной в саду, то первому стражнику досталось х /2 яблок, второй получил х /4 яблок, третий - х/8 яблок и четвертый - х/16 яблок. Так как х/16 = 10, то х = 160. Следовательно, женщина собрала в саду 160 яблок.
Загадочная
8 Августа 2015
Загадка №3953.
Если человек идет на работу пешком, а назад едет на транспорте, то в целом на дорогу тратит полтора часа. Если же в оба конца он едет на транспорте, то весь путь занимает у него 30 минут. Сколько времен нужно человеку на дорогу, если на работу и назад он пойдет пешком?
Ответ: Пользуясь транспортом, человек тратит на путь туда и обратно 30 минут. Поэтому путь в одну сторону занимает 15 минут. Выходит, пешком он может добраться до работы за 1 час и 30 минут - 15 минут = 1 час и 15 минут. Весь путь займет вдвое больше времени - 2 часа и 30 минут.
Зиночка
25 Июля 2015
Загадка №3982.
Длина и 1/4 ширины вместе составляют 7 ладоней, а длина и ширина вместе - 10 ладоней. Сколько ладоней составляют длина и ширина отдельно?
Ответ: Пусть ширина составляет х ладоней, длина − y ладоней. Тогда
(x/4) + y = 7, (1)
х + у = 10, (2)
х = 10 − у. (2')
Подставляя (2') в (1), получаем
(10−y)/4 + y = 7,
у = 6.
Потом из (1) находим
(x/4) + 6 = 7, x = 4.
(x/4) + y = 7, (1)
х + у = 10, (2)
х = 10 − у. (2')
Подставляя (2') в (1), получаем
(10−y)/4 + y = 7,
у = 6.
Потом из (1) находим
(x/4) + 6 = 7, x = 4.
Алексеевич
19 Июля 2015
Загадка №3972.
Сколько раз на протяжении суток минутная и часовая стрелки часов образуют прямой угол?
Ответ: На протяжении суток минутная и часовая стрелки образуют прямой угол 44 раза. Есть два решения этой задачи.
1) Логическое. В сутки часовая стрелка делает 2 оборота, а минутная - 24 . Отсюда минутная стрелка обгоняет часовую 22 раза и каждый раз с часовой стрелкой образуется по два прямых угла, т. е. ответ - 44.
2) Математическое. За 1 час часовая стрелка описывает угол 30°, а за 1 мин. − угол 0,5°. Минутная стрелка за 1 мин. описывает угол 6°. Так как 90 : (6 − 0,5) = 16 (4 / 11), минутная и часовая стрелки образуют прямой угол в первый раз через 16 (4 / 11) мин. после того, как обе будут стоять на 12. Так как n × 16 (4/11) = 24 × 60, мы получаем n = 88 (в это число входят углы в 0°, 90°, 180° і 270°, образованные минутной и часовой стрелками).
1) Логическое. В сутки часовая стрелка делает 2 оборота, а минутная - 24 . Отсюда минутная стрелка обгоняет часовую 22 раза и каждый раз с часовой стрелкой образуется по два прямых угла, т. е. ответ - 44.
2) Математическое. За 1 час часовая стрелка описывает угол 30°, а за 1 мин. − угол 0,5°. Минутная стрелка за 1 мин. описывает угол 6°. Так как 90 : (6 − 0,5) = 16 (4 / 11), минутная и часовая стрелки образуют прямой угол в первый раз через 16 (4 / 11) мин. после того, как обе будут стоять на 12. Так как n × 16 (4/11) = 24 × 60, мы получаем n = 88 (в это число входят углы в 0°, 90°, 180° і 270°, образованные минутной и часовой стрелками).
Загадочник
12 Июля 2015
Загадка №3952.
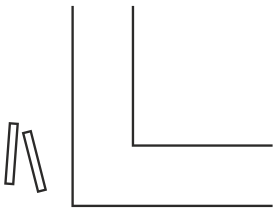
Ответ: Стоит глянуть на приведенный здесь рисунок, что бы понять, как решается задание. Что касается математического доказательства возможности подобной переправы, то он выплывает из неравенства 2√2<3 и делается явным, если принять ширину равную трем каким-либо единицам. 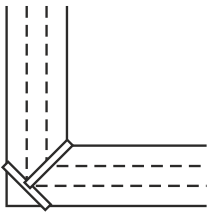

Любитель загадок
4 Июля 2015
Загадка №3979.
На часах ровно 9. Через сколько минут стрелки часов (минутная и часовая) совпадут?
Ответ: Если часовая стрелка до того, как обе стрелки совпадут, успеет пройти х минутных делений, то минутная стрелка за то же время пройдет (45+x) минутных делений. Из-за того, что за одно и то же время часовая стрелка проходит 1/12 того, что проходит минутная, мы можем составить уравнение х=(45+x)/12, откуда х = 4 целых и (1/11).
Минутная стрелка совпадает с часовой через 49 целых и (1/11) хв.
Минутная стрелка совпадает с часовой через 49 целых и (1/11) хв.
Ольга
25 Июня 2015
Загадка для детей №2429.
Какие три числа при сложении и при умножении дают один и тот же результат?
Ответ: 1 + 2 + 3 = 6, 1 * 2 * 3 = 6
Хулиганка
22 Июня 2015
Загадка с подвохом №2220.
Ничего не пишите и не используйте калькулятор. Возьмите 1000. Прибавьте 40. Прибавьте еще тысячу. Прибавьте 30. Еще 1000. Плюс 20. Плюс 1000. И плюс 10. Что получилось?
Ответ: 5000? Неверно. Правильный ответ 4100. Попробуйте пересчитать на калькуляторе
Зиночка
20 Июня 2015
Загадка №4006.
45 % поступлений лотереи тратится на выплату выигрышей.Сколько билетов стоимостью по 5 франков должны распространить организаторы лотереи, если на выплату выигрыша предусматривается потратить 87 300 франков?
Ответ: Пусть х − число билетов лотереи, которые подлежат распространению. Тогда
5х = 87 300 × 100 / 45 = 194 000,
х = 38 800.
Значит, что бы потратить намеченную сумму в 87 300 франков на выплату выигрышей, организаторам лотереи необходимо продать 38 800 билетов стоимостью по 5 франков.
5х = 87 300 × 100 / 45 = 194 000,
х = 38 800.
Значит, что бы потратить намеченную сумму в 87 300 франков на выплату выигрышей, организаторам лотереи необходимо продать 38 800 билетов стоимостью по 5 франков.
Любитель загадок
15 Июня 2015
Загадка №3984.
Один биолог открыл удивительную разновидность амеб. Каждая из них через минуту делится на две. В пробирку биолог кладет одну амебу, и через час вся пробирка оказывается заполненной амебами. Сколько нужно было бы времени, чтобы вся пробирка заполнилась амебами, если бы в нее сначала положили не одну амебу, а две?
Ответ: 59 минут.
Загадочная
7 Июня 2015
Загадка №3975.
На часах Клауса минутные деления нанесено небольшими штрихами. Глянув на часы на шестом часу после полудня, Клаус обнаружил, что большая стрелка отстает от малой на 3 деления.Сколько было на часах?
Ответ: В 5.00 минутную стрелку отделяют от часовой 25 минутных делений. В тот момент, когда Клаус глянул на часы, длинная стрелка отставала от малой лишь на 3 деления и, следовательно, успела пройти 22 деления. За 1 мин. длинная стрелка проходит 1 деление, а малая 1/12 делений. Следовательно, за 1 мин. минутная стрелка догоняет часовую на 1 - 1/12 = 11/12 делений, а для того, чтобы пройти 22 деления, минутной стрелке понадобится 22 : (11/12) = 24 мин.
Следовательно, Клаус глянул на часы в 5.24.
Следовательно, Клаус глянул на часы в 5.24.
Загадочная
7 Июня 2015
Загадка №2347.
Суммарный возраст отца и сына - 66 лет. Возраст отца - это возраст сына, записанный справа налево. Сколько лет каждому?
Ответ: 51 и 15, 42 и 24, 60 и 06
Света
6 Июня 2015
Загадка №3965.
Десять собак и кошек накормили 56-ю галетами. Каждой собаке досталось 6 галет, каждой кошке - пять. Сколько было собак и скольких кошек? Попробуйте решить задание, не используя ни систему уравнений, ни перебор вариантов.
Ответ: Если бы были только собаки, то было бы съедено 60 галет. Но поскольку было съедено на 4 галеты меньше, следовательно, кошек было 4 (по одной отсутствующей галете до 60), значит, собак было 10 - 4 = 6.
Валентин
5 Июня 2015
Загадка с подвохом №4021.
Что больше: сума всех цифр или их произведение?
Ответ: Сумма. Произведение будет равно «0», так как будет же умножение и на число «0».
Любитель загадок
28 Мая 2015
Загадка №3994.
Одно швейцарское общество насчитывает 50 членов. Родной язык всех 50 членов общества - немецкий, но 20 из них говорят еще и на итальянском, 35 из них владеют французским и 10 не знают ни итальянского, ни французского.Сколько членов общества говорят и французским и итальянским?
Ответ: Из 50 членов общества 10 говорят только на родном (немецком) языке. Другие 40 членов общества, кроме родного языка, владеют также французским или итальянским языком. Так как 20 + 35 = 55, а 55 – 40 = 15, то делаем вывод, что 15 членов общества говорят и на французском и на итальянским.
Валентин
28 Мая 2015
Загадка №3968.
Один кирпич весит 1 килограмм и еще пол кирпича. Сколько весит один кирпич?
Ответ: 2 кг.
Люся
26 Мая 2015
Загадка №3999.
Какой-то математик насчитал на выгоне 70 коров. «Какую часть от всего табуна составляют эти коровы?» - спросил математик у пастуха. «Я выгнал пастись две трети от трети всего табуна», - отвечал пастух. Сколько голов скота насчитывается во всем табуне?
Ответ: Пусть х − число голов скота во всем табуне. Тогда (2/3)×(1/3)х = 70, откуда после эквивалентных преобразований (2/9)х =70, 2х = 630 находим: х = 315. Значит, во всем табуне было 315 голов скота.
Загадки на связанные темы: