Место для рекламы
Математические - Загадки для взрослых (Страница 3)
Загадки для взрослых - Математические
Любитель загадок
28 Августа 2015
Загадка №4033.
Эта задача известна с давних времен. Во вьетнамских деревнях старики-рисоводы любят задавать ее молодежи. Так задача переходит от поколения к поколению.Для кормления 100 буйволов заготовили 100 охапок сена.
- Стоящий молодой буйвол съедает 5 охапок сена.
- Лежащий молодой буйвол съедает 3 охапки сена.
- Старые буйволы втроем съедают 1 охапку сена.
Сколько молодых буйволов стоят, сколько лежат и сколько буйволов старых?
Ответ: Пусть х – число стоящих, у – число лежащих молодых буйволов и z – число старых буйволов. Тогда
х + у + z = 100, (1)
5х +3 у + (z/3) = 100, (2)
у = 25 – (7х/4).
Так как х и у – натуральные числа, последнее равенство выполняется только при х = 0, 4, 8, 12. Задача допускает поэтому следующие четыре решения:
x = 0, 4, 8, 12
y = 25, 18, 11, 4
z = 75, 78, 81, 84
х + у + z = 100, (1)
5х +3 у + (z/3) = 100, (2)
у = 25 – (7х/4).
Так как х и у – натуральные числа, последнее равенство выполняется только при х = 0, 4, 8, 12. Задача допускает поэтому следующие четыре решения:
x = 0, 4, 8, 12
y = 25, 18, 11, 4
z = 75, 78, 81, 84
Любитель загадок
22 Февраля 2018
Загадка №6841.

1 + 4 = 5
2 + 5 = 12
3 + 6 = 21
8 + 11 = ?
Ответ: Существуют как минимум 2 очевидных решения этой задачки.
В первом варианте к слагаемым нужно добавлять сумму предыдущего равенства:
1 + 4 = 5
5 + 2 + 5 = 12
12 + 3 + 6 = 21
21 + 8 + 11 = 40
Но можно найти и другую последовательность, для этого второе слагаемое нужно умножить на первое и прибавить первое слагаемое:
1 + (4 × 1) = 5
2 + (5 × 2) = 12
3 + (6 × 3) = 21
8 + (8 × 11) = 96
В первом варианте к слагаемым нужно добавлять сумму предыдущего равенства:
1 + 4 = 5
5 + 2 + 5 = 12
12 + 3 + 6 = 21
21 + 8 + 11 = 40
Но можно найти и другую последовательность, для этого второе слагаемое нужно умножить на первое и прибавить первое слагаемое:
1 + (4 × 1) = 5
2 + (5 × 2) = 12
3 + (6 × 3) = 21
8 + (8 × 11) = 96
Сергей
8 Февраля 2018
Загадка №6782.
У женщины спросили: "Сколько Вам лет?". Она ответила: "30, не считая суббот и воскресений". Сколько ей лет?
Ответ: Женщине 42 года.
Решение. Без суббот и воскресений - значит считать каждые 5 дней в неделю, т.е. лишь 5/7 жизни. Если 5/7 это 30 лет, то верный ответ 30 × 7 / 5 = 42.
Решение. Без суббот и воскресений - значит считать каждые 5 дней в неделю, т.е. лишь 5/7 жизни. Если 5/7 это 30 лет, то верный ответ 30 × 7 / 5 = 42.
Валентин
23 Августа 2015
Загадка №4008.
Одна женщина отправилась в сад собирать яблоки. Чтобы выйти из сада, ей нужно было пройти через четверо дверей, у каждой из которых стоял стражник. Стражнику у первых дверей женщина отдала половину сорванных ею яблок. Дойдя до второго стражника, женщина отдала ему половину яблок, которые остались. Так же она сделала и с третьим стражником; а когда она поделилась яблоками со стражником у четвертых дверей (с которым она сделали как и с предыдущими) то у нее осталось лишь 10 яблок. Сколько яблок она собрала в саду?
Ответ: Если х - число яблок, собранных женщиной в саду, то первому стражнику досталось х /2 яблок, второй получил х /4 яблок, третий - х/8 яблок и четвертый - х/16 яблок. Так как х/16 = 10, то х = 160. Следовательно, женщина собрала в саду 160 яблок.
Любитель загадок
25 Апреля 2025
Загадка №9736.

Ответ: Можно решить логически, не составляя уравнений. Если бы все машины были легковыми, то колес было бы 750*4=3000. Лишние 24 колеса "набегают" из-за наличия грузовых, у которых по 6-4=2 колеса "лишних".
Значит, грузовых 24/2=12
А легковых - 738
---
Либо составляем систему уравнений:
4*х + 6*y = 3024
x + y = 750
Решаем и получаем Y=12, X=238
Значит, грузовых 24/2=12
А легковых - 738
---
Либо составляем систему уравнений:
4*х + 6*y = 3024
x + y = 750
Решаем и получаем Y=12, X=238
Любитель загадок
18 Апреля 2025
Загадка №9735.
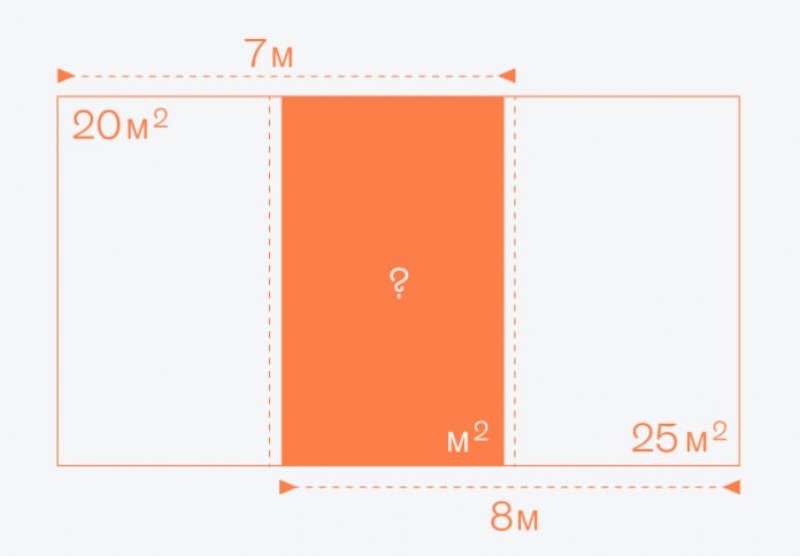
Ответ: Пусть x - длина маленького прямоугольника, а y - ширина прямоугольника.
Тогда:
(8-x)y=25
(7-x)y=20
Решаем уравнения и получаем:
x=3 y=5
S=3×5=15
Тогда:
(8-x)y=25
(7-x)y=20
Решаем уравнения и получаем:
x=3 y=5
S=3×5=15
Художница
12 Марта 2015
Загадка №3990.
Нам обоим вместе 63 года. В настоящий момент мне лет вдвое больше, чем вам было тогда, когда мне было столько лет, сколько вам в настоящий момент.Сколько мне лет и сколько вам лет?
Ответ: В настоящий момент мне 36, а вам 27. А когда-то мне было 27, а вам 18.
Любитель загадок
16 Февраля 2016
Загадка №4079.
Фермер приехал на рынок продавать яблоки. Первый покупатель приобрел сразу половину всех яблок и еще пол-яблока. Второй – половину от того, что осталось и также пол-яблока. Третий только один фрукт. После этого весь товар фермера закончился. Сколько же яблок было изначально?
Ответ: У фермера было семь яблок. Первый покупатель взял 4, второй – 2, третьему осталось – одно.
Хулиганка
4 Февраля 2015
Загадка №3977.
Три года назад Настя была в 7 раз старше своей сестры Вероники. Два года назад Настя была в 4 раза старше Вероника. Год назад Настя была в 3 раза старше Вероника.Сколько лет Насте и Веронике?
Ответ: Насте 10 лет, а Веронике 4 года. Доказательство: пусть в настоящий момент Насте x лет, а Веронике y. Тогда, три года назад можно было бы записать: x-3=7*(y-3), два года тому назад: x-2=4*(y-2), год назад: x-1=3*(y-1). Из последнего уравнения выплывает, что x=3*y-2. Подставляя это во второе уравнение, получаем: 3*y-2-2=4*(y-2) откуда y=4. Подставляя значение y в уравнение для x, получаем: x=3*4-2=10.
Любитель загадок
23 Марта 2025
Загадка №9718.
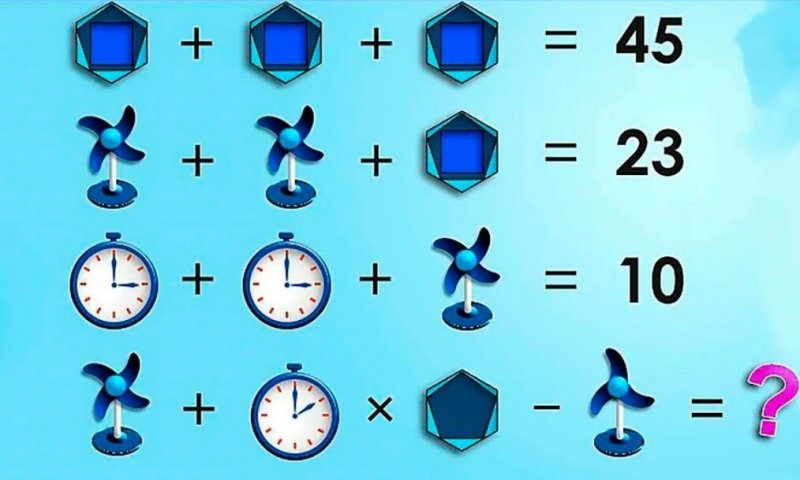
Ответ: 4 + (11х2) - 3 = 23
В данной загадке важно учитывать количество углов, показания часов и количество лопастей.
В данной загадке важно учитывать количество углов, показания часов и количество лопастей.
Хулиганка
28 Ноября 2015
Загадка №3966.
Перед вами выражение 987654321=100. Сделайте его верным, используя 4 знака "+" или "-" в его левой части.
Ответ: 98 - 76 + 54 + 3 + 21 = 100
Загадочная
8 Августа 2015
Загадка №3953.
Если человек идет на работу пешком, а назад едет на транспорте, то в целом на дорогу тратит полтора часа. Если же в оба конца он едет на транспорте, то весь путь занимает у него 30 минут. Сколько времен нужно человеку на дорогу, если на работу и назад он пойдет пешком?
Ответ: Пользуясь транспортом, человек тратит на путь туда и обратно 30 минут. Поэтому путь в одну сторону занимает 15 минут. Выходит, пешком он может добраться до работы за 1 час и 30 минут - 15 минут = 1 час и 15 минут. Весь путь займет вдвое больше времени - 2 часа и 30 минут.
Наталья
13 Февраля 2015
Загадка №3998.
Древняя задача на бытовую тему. Ее задавал своим ученикам учитель арифметики Якоб из Кобурга, чей учебник был напечатан в 1599 г. во Франкфурте.Расстояние между 2 городами составляет 260 миль. Из обоих городов навстречу друг другу выходят 2 гонца. Один из них ежедневно проходить на 2 мили больше, чем другой. Через 12 дней гонцы встречаются.
Сколько миль проходить ежедневно каждый гонец?
Ответ: Пусть y − число миль, которое проходит за день один, а х − другой гонец. Тогда
y = х + 2, (1)
12х +12y = 260. (2)
Подставляя (1) в (2), получаем
12х +12(х+2) = 260,
откуда
х = 9 та 5/6.
Таким образом, один гонец проходил за день 9 и 5/6 миль, а другой − 11 и 5/6 миль.
y = х + 2, (1)
12х +12y = 260. (2)
Подставляя (1) в (2), получаем
12х +12(х+2) = 260,
откуда
х = 9 та 5/6.
Таким образом, один гонец проходил за день 9 и 5/6 миль, а другой − 11 и 5/6 миль.
Любитель загадок
19 Октября 2024
Загадка №9630.
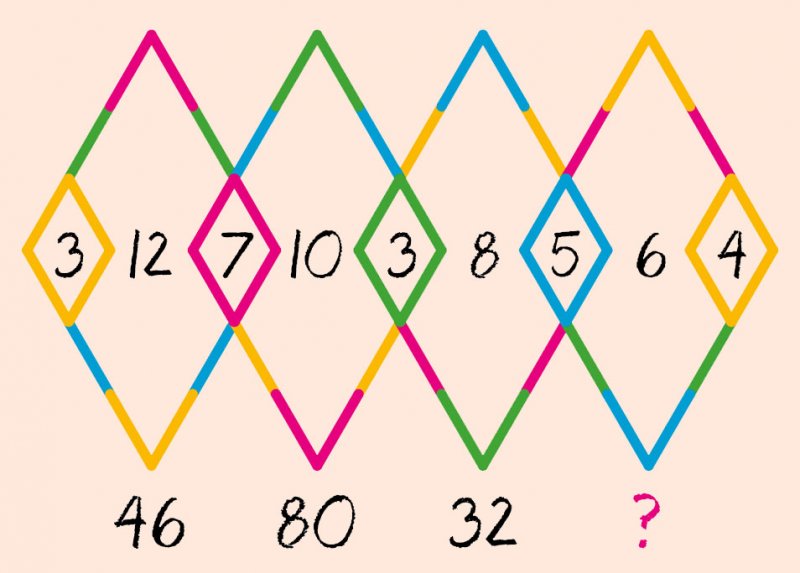
Ответ: 39.
3x12=36+(3+7)=46;
7x10=70+(7+3)=80;
3x8=24+(3+5)=32;
5x6=30+(5+4)=39
3x12=36+(3+7)=46;
7x10=70+(7+3)=80;
3x8=24+(3+5)=32;
5x6=30+(5+4)=39
Любитель загадок
1 Ноября 2024
Загадка №9646.
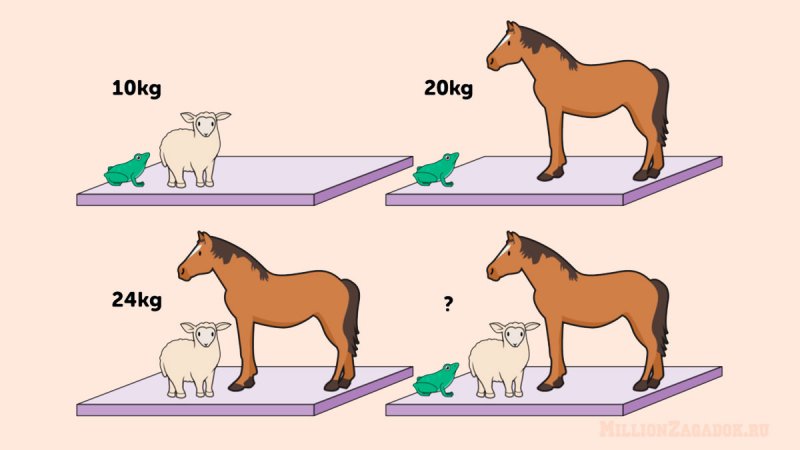
Ответ: 27 кг. Существует два способа решения этой загадки.
Первый способ — более сложный. Если вес овцы с лошадью составляет 24 кг, а вес лягушки с лошадью — 20 кг, то разница в весе между овцой и лягушкой равна 4 кг. Следовательно, вес овцы составляет 7 кг, а вес лягушки — 3 кг. Вес лошади в этом случае будет равен 17 кг. Таким образом, общий вес овцы, лошади и лягушки составляет 27 кг.
Второй способ — более простой, но требующий сообразительности. Обратите внимание на картинку: каждое животное изображено дважды. Это означает, что можно сложить все результаты, полученные на весах, и разделить их на два. В результате мы получим, что вес одной лошади, одной овцы и одной лягушки составляет 27 кг.
Первый способ — более сложный. Если вес овцы с лошадью составляет 24 кг, а вес лягушки с лошадью — 20 кг, то разница в весе между овцой и лягушкой равна 4 кг. Следовательно, вес овцы составляет 7 кг, а вес лягушки — 3 кг. Вес лошади в этом случае будет равен 17 кг. Таким образом, общий вес овцы, лошади и лягушки составляет 27 кг.
Второй способ — более простой, но требующий сообразительности. Обратите внимание на картинку: каждое животное изображено дважды. Это означает, что можно сложить все результаты, полученные на весах, и разделить их на два. В результате мы получим, что вес одной лошади, одной овцы и одной лягушки составляет 27 кг.
Валентин
9 Ноября 2015
Загадка №3955.
В зоомагазине продают больших и маленьких птиц. Большая птица вдвое дороже маленькой. Леди, которая зашла в магазин, купила 5 больших птиц и 3 маленьких. Если бы она вместо этого купила 3 больших птицы и 5 маленьких, то потратила бы на 20 долларов меньше. Сколько стоит каждая птица?
Ответ: Цена большой птицы 20 долларов, а маленькой — 10 долларов. Решение: пусть цена маленькой птицы будет x, тогда большой будет y=2x. Леди купила 5 больших и три маленьких, то есть 5y + 3x. Если бы она купила 3 больших и пять маленьких, то есть 3y + 5x, то витратила б на 20 то потратила бы на 20 долларов меньше. Получаем: (5y + 3x) - (3y + 5x) = 20 -> 2y - 2x = 20 -> 4x - 2x = 20 -> x = 10 -> y = 2x = 20.
Зиночка
25 Июля 2015
Загадка №3982.
Длина и 1/4 ширины вместе составляют 7 ладоней, а длина и ширина вместе - 10 ладоней. Сколько ладоней составляют длина и ширина отдельно?
Ответ: Пусть ширина составляет х ладоней, длина − y ладоней. Тогда
(x/4) + y = 7, (1)
х + у = 10, (2)
х = 10 − у. (2')
Подставляя (2') в (1), получаем
(10−y)/4 + y = 7,
у = 6.
Потом из (1) находим
(x/4) + 6 = 7, x = 4.
(x/4) + y = 7, (1)
х + у = 10, (2)
х = 10 − у. (2')
Подставляя (2') в (1), получаем
(10−y)/4 + y = 7,
у = 6.
Потом из (1) находим
(x/4) + 6 = 7, x = 4.
Люся
26 Мая 2015
Загадка №3999.
Какой-то математик насчитал на выгоне 70 коров. «Какую часть от всего табуна составляют эти коровы?» - спросил математик у пастуха. «Я выгнал пастись две трети от трети всего табуна», - отвечал пастух. Сколько голов скота насчитывается во всем табуне?
Ответ: Пусть х − число голов скота во всем табуне. Тогда (2/3)×(1/3)х = 70, откуда после эквивалентных преобразований (2/9)х =70, 2х = 630 находим: х = 315. Значит, во всем табуне было 315 голов скота.
Любитель загадок
15 Октября 2024
Загадка №9626.
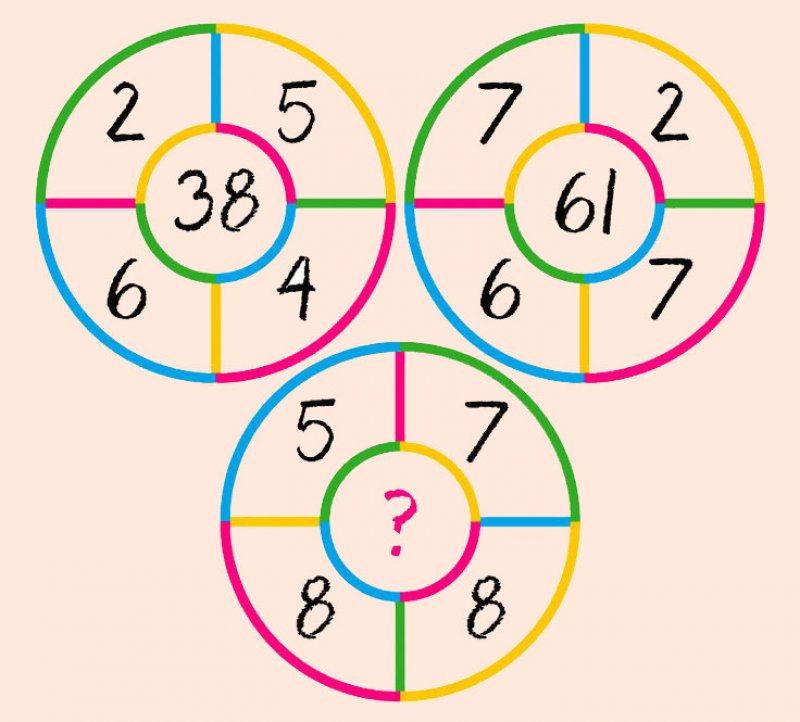
Ответ: 5*8 + 8*7 = 96
Зиночка
17 Апреля 2015
Загадка №4001.
Один раз мы поневоле стали свидетелями следующего разговора.- Правильно ли я тебя понял? Ты утверждаешь, что ты являешься членом шахматного клуба вдвое дольше, чем я.
- Полностью правильно.
- Но насколько я помню, раньше ты говорил, что был членом шахматного клуба втрое дольше, чем я?
- Два года тому назад? Но тогда мой стаж как члена клуба действительно был в 3 раза больше твоего, а теперь лишь в 2 раза.
Сколько лет каждый из двух собеседников являются членами шахматного клуба?
Ответ: Условия задачи позволяют записать уравнения
(x − стаж одного собеседника, y − другого):
y = 2 x,
y − 2х 3(х − 2),
откуда x = 4, y = 8.
Значит, один сотрудник в шахматном клубе уже 8 лет, другой − 4 года.
(x − стаж одного собеседника, y − другого):
y = 2 x,
y − 2х 3(х − 2),
откуда x = 4, y = 8.
Значит, один сотрудник в шахматном клубе уже 8 лет, другой − 4 года.
Зиночка
20 Июня 2015
Загадка №4006.
45 % поступлений лотереи тратится на выплату выигрышей.Сколько билетов стоимостью по 5 франков должны распространить организаторы лотереи, если на выплату выигрыша предусматривается потратить 87 300 франков?
Ответ: Пусть х − число билетов лотереи, которые подлежат распространению. Тогда
5х = 87 300 × 100 / 45 = 194 000,
х = 38 800.
Значит, что бы потратить намеченную сумму в 87 300 франков на выплату выигрышей, организаторам лотереи необходимо продать 38 800 билетов стоимостью по 5 франков.
5х = 87 300 × 100 / 45 = 194 000,
х = 38 800.
Значит, что бы потратить намеченную сумму в 87 300 франков на выплату выигрышей, организаторам лотереи необходимо продать 38 800 билетов стоимостью по 5 франков.
Любитель загадок
23 Апреля 2018
Загадка №6894.

Какой палец будет по счёту 1992-м?
Ответ: Безымянный
Загадочник
12 Июля 2015
Загадка №3952.
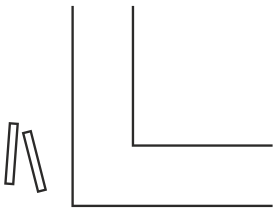
Ответ: Стоит глянуть на приведенный здесь рисунок, что бы понять, как решается задание. Что касается математического доказательства возможности подобной переправы, то он выплывает из неравенства 2√2<3 и делается явным, если принять ширину равную трем каким-либо единицам. 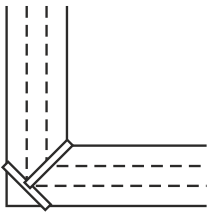

Валентин
28 Апреля 2015
Загадка №4036.
Во время летнего пикника четыре супружеские пары выпили 32 бутылки лимонада. Жены выпили: Жанна – 1 бутылку, Жаклин – 2 бутылки, Колетта – 3 бутылки и Анетта – 4 бутылки. Мужья не уступили женам: месье Пон выпил столько же, сколько его жена, месье Дюбуа – вдвое больше своей жены, месье Пейзан – втрое и месье Фонтен – вчетверо больше своих жен.Как зовут мадам Пон, Дюбуа, Пейзан и Фонтен?
Ответ: Пусть х, у, z и u – число бутылок лимонада, которое выпили соответственно жены месье Попа, Дюбуа, Пейзана и Фонтена. Всего жены выпили
х + у + z + u = 10
бутылок лимонада. Их мужья выпили
х + 2у + 3z + 4u
бутылок лимонада, а четыре супружеские пары вместе опустошили
2х +3 у + 4z + 5u = 32
бутылки лимонада. Подставляя
u = 10 - х - у - z, получаем
18 = 3х+2 у + z .
Числа х и z должны быть либо оба четными, либо оба нечетными. Значения х=1 и х=2 отпадают, так как каждое из чисел у и z не превосходит 4. При х=4 мы получили бы z = 2 и у = 2, что невозможно, так как х, у, z и u – различные числа. Следовательно, задача допускает единственное решение:
х = 3, z = 1, у = 4, u = 2;
х = 3 (Колетта Пон), у = 4 (Анетта Дюбуа), z = 1 (Жанна Пейзан), u = 2 (Жаклин Фонтен).
х + у + z + u = 10
бутылок лимонада. Их мужья выпили
х + 2у + 3z + 4u
бутылок лимонада, а четыре супружеские пары вместе опустошили
2х +3 у + 4z + 5u = 32
бутылки лимонада. Подставляя
u = 10 - х - у - z, получаем
18 = 3х+2 у + z .
Числа х и z должны быть либо оба четными, либо оба нечетными. Значения х=1 и х=2 отпадают, так как каждое из чисел у и z не превосходит 4. При х=4 мы получили бы z = 2 и у = 2, что невозможно, так как х, у, z и u – различные числа. Следовательно, задача допускает единственное решение:
х = 3, z = 1, у = 4, u = 2;
х = 3 (Колетта Пон), у = 4 (Анетта Дюбуа), z = 1 (Жанна Пейзан), u = 2 (Жаклин Фонтен).
Художница
17 Января 2016
Загадка №3976.
Летела стая гусей, увидел их дядька и говорит:– По-видимому, вас сто!
А гуси и отвечают:
– «Если бы нас столько,
Да еще бы столько,
И половину как столько,
И четверть как столько,
И ты бы с нами, – тогда бы сто и было».
Сколько гусей?
Ответ: 36 гусей: 36+36+18+9+1=100.
Админ
16 Октября 2015
Загадка №4000.
Это не столько загадка, сколько фокус, основанный на математике. Попросите кого-нибудь задумать (написать, чтобы вы не видели) пятизначное число, потом умножить его на девять и зачеркнуть любую цифру. А теперь попросите сложить оставшиеся цифры и назвать сумму. После чего вы без труда угадаете зачеркнутую цифру.
Ответ: В основе фокуса лежит правило - что если число делиться на 9, то и его сумма делится на 9. Когда вычеркивают цифру то сумма становится не кратна 9 и вам надо найти ближайшее число кратное девяти. Разница между названной суммой и этим числом и будет вычеркнутое число.
Админ
10 Апреля 2015
Загадка №3980.
В одном буддийском храме на высоте 100 метров к потолку приделаны два золотых каната, длиной по 100 метров каждый.Оба каната свисают до пола. Они висят на близком расстоянии, например, - полметра. В храм заходит Вор - ловкий акробат, который умеет лазить по канатам и отрезать их. Если Вор свалится на землю с высоты менее 10 метров, то он доволен. Если с большей высоты – умирает (лечение ему уже не поможет).
Как ему удалось забрать из храма не менее 190 метров золотого каната, а не только 110? (канаты считать легкими).
Ответ: Влезает по одному из канатов на высоту 95 метров и отрезает от другого 95 метров. Часть в 5 метров, которая осталась висеть, привязывает к первому канату в точке деления на 5 и 95 метров. Выходит, петля создана связанными 5 метрами первого каната и 5 метрами второго каната. После чего, свободный конец полученного 195 метрового каната пропускает через петлю. Вверху он режет первый канат в точке 5 и 95 метров. Выходит, что через петлю 10 метров свисает канат длиной 190 метров. Вор спускается вниз и забирает 190 метров.
Загадочная
27 Февраля 2015
Загадка №3981.
Ванная заполняется холодной водой за 6 минут 40 секунд, горячей за 8 минут. Кроме того, если из полной ванны вынуть пробку, вода вытечет за 13 минут 20 секунд.Сколько времени понадобится, чтобы наполнить ванную полностью, при условии, что открыты оба крана, но ванная не закрыта пробкой?
Ответ: Введем обозначения: V - объем ванной, t1 - время заполнения холодной водой, t2 – горячей водой; t3 – время, за которое вода полностью вытечет,
- скорость течения холодной воды;
- горячей воды;
- скорость, с которой вода вытекает при закрытых кранах.
Тогда, если все открыто, скорость, с которой наполняется ванная:
Значит, необходимое время на заполнение ванны, если все открыто, будет:
Необходимо 300 сек. = 5 минут.
- скорость течения холодной воды;
- горячей воды;
- скорость, с которой вода вытекает при закрытых кранах.
Тогда, если все открыто, скорость, с которой наполняется ванная:
Значит, необходимое время на заполнение ванны, если все открыто, будет:
Необходимо 300 сек. = 5 минут.
Художница
11 Января 2016
Загадка №4004.
Стая голубей подлетела к высокому дереву. Часть голубей села на ветвях, а другая расположилась под деревом. Голуби, которые сидели на ветвях, говорят к тем, что внизу: «Если бы один из вас взлетел к нам, то вас стало бы втрое меньше, чем нас всех вместе, а если бы один из нас взлетел к вам, то нас с вами стало бы поровну. Сколько голубей сидело на ветвях и сколько под деревом?
Ответ: Пусть х − число голубей, что сели на дерево, а y − число голубей, что разместились под деревом. Тогда
y – 1 = (x + y) / 3
и, кроме того, х – 1 = y +1, тобто х = y + 2.
Подставляя х = y + 2 в первое уравнение, получаем
(y – 1) × 3 = y + 2 + y,
3y – 3 = 2y + 2,
y = 5.
Значит, х = y + 2 = 7.
Отсюда, 7 голубей сели на дерево, а 5 голубей разместились под деревом.
y – 1 = (x + y) / 3
и, кроме того, х – 1 = y +1, тобто х = y + 2.
Подставляя х = y + 2 в первое уравнение, получаем
(y – 1) × 3 = y + 2 + y,
3y – 3 = 2y + 2,
y = 5.
Значит, х = y + 2 = 7.
Отсюда, 7 голубей сели на дерево, а 5 голубей разместились под деревом.
Любитель загадок
1 Ноября 2024
Загадка №9645.

повторяться!
Ответ: 6/1,2 = 5
Загадки для взрослых на связанные темы: